|
|
|
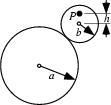
|
The Roulette traced by a point ![]() attached to a Circle of radius
attached to a Circle of radius ![]() rolling around the outside of a fixed
Circle of radius
rolling around the outside of a fixed
Circle of radius ![]() . These curves were studied by Dürer (1525), Desargues (1640), Huygens
. These curves were studied by Dürer (1525), Desargues (1640), Huygens ![]() (1679),
Leibniz,
(1679),
Leibniz, ![]() Newton
Newton ![]() (1686), L'Hospital
(1686), L'Hospital ![]() (1690), Jakob Bernoulli
(1690), Jakob Bernoulli ![]() (1690), la Hire (1694), Johann Bernoulli
(1690), la Hire (1694), Johann Bernoulli ![]() (1695), Daniel Bernoulli
(1695), Daniel Bernoulli ![]() (1725), Euler
(1725), Euler ![]() (1745, 1781). An epitrochoid appears in Dürer's work Instruction in Measurement with Compasses
and Straight Edge (1525). He called epitrochoids Spider Lines because the lines he used to construct the curves looked
like a spider.
(1745, 1781). An epitrochoid appears in Dürer's work Instruction in Measurement with Compasses
and Straight Edge (1525). He called epitrochoids Spider Lines because the lines he used to construct the curves looked
like a spider.
The parametric equations for an epitrochoid are
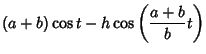 |
|||
 |
See also Epicycloid, Hypotrochoid, Spirograph, Trochoid
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 168-170, 1972.
Lee, X. ``Epitrochoid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Epitrochoid_dir/epitrochoid.html.
Lee, X. ``Epitrochoid and Hypotrochoid Movie Gallery.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/EpiHypoTMovieGallery_dir/epiHypoTMovieGallery.html.