|
|
|
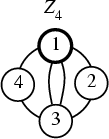
One of the two groups of Order 4. Like
![]() , it is Abelian,
but unlike
, it is Abelian,
but unlike
![]() , it is a Cyclic. Examples include the Point Groups
, it is a Cyclic. Examples include the Point Groups ![]() and
and
![]() and the Modulo Multiplication Groups
and the Modulo Multiplication Groups ![]() and
and ![]() . Elements
. Elements ![]() of
the group satisfy
of
the group satisfy ![]() , where 1 is the Identity Element, and two of the elements satisfy
, where 1 is the Identity Element, and two of the elements satisfy ![]() .
.
The Cycle Graph is shown above. The Multiplication Table for this group may be written in three equivalent
ways--denoted here by ![]() ,
, ![]() , and
, and ![]() --by permuting the symbols used for the group elements.
--by permuting the symbols used for the group elements.
| 1 | ||||
| 1 | 1 | |||
| 1 | ||||
| 1 | ||||
| 1 |
The Multiplication Table for ![]() is obtained from
is obtained from ![]() by interchanging
by interchanging ![]() and
and ![]() .
.
|
|
1 | |||
| 1 | 1 | |||
| 1 | ||||
| 1 | ||||
| 1 |
The Multiplication Table for ![]() is obtained from
is obtained from ![]() by interchanging
by interchanging ![]() and
and ![]() .
.
| 1 | ||||
| 1 | 1 | |||
| 1 | ||||
| 1 | ||||
| 1 |
The Conjugacy Classes of ![]() are
are ![]() ,
, ![]() ,
,
| (1) | |||
| (2) | |||
| (3) |
| (4) | |||
| (5) | |||
| (6) |
The group may be given a reducible representation using Complex Numbers
| (7) | |||
| (8) | |||
| (9) | |||
| (10) |
| (11) | |||
![$\displaystyle \left[\begin{array}{cc}0 & -1 \\ 1 & 0 \end{array}\right]$](f_1250.gif) |
(12) | ||
![$\displaystyle \left[\begin{array}{cc}-1 & 0 \\ 0 & -1 \end{array}\right]$](f_1203.gif) |
(13) | ||
![$\displaystyle \left[\begin{array}{cc}0 & 1 \\ -1 & 0 \end{array}\right].$](f_1251.gif) |
(14) |
See also Finite Group Z2Z2
|
|
|
© 1996-9 Eric W. Weisstein