|
|
|
A Finite Group ![]() of Residue Classes prime to
of Residue Classes prime to ![]() under multiplication mod
under multiplication mod ![]() .
. ![]() is
Abelian of Order
is
Abelian of Order ![]() , where
, where ![]() is the Totient Function.
The following table gives the modulo multiplication groups of small orders.
is the Totient Function.
The following table gives the modulo multiplication groups of small orders.
| Group | Elements | ||
|
|
1 | 1 | |
| 2 | 1, 2 | ||
| 2 | 1, 3 | ||
| 4 | 1, 2, 3, 4 | ||
| 2 | 1, 5 | ||
| 6 | 1, 2, 3, 4, 5, 6 | ||
|
|
4 | 1, 3, 5, 7 | |
| 6 | 1, 2, 4, 5, 7, 8 | ||
| 4 | 1, 3, 7, 9 | ||
| 10 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 | ||
|
|
4 | 1, 5, 7, 11 | |
| 12 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 | ||
| 6 | 1, 3, 5, 9, 11, 13 | ||
|
|
8 | 1, 2, 4, 7, 8, 11, 13, 14 | |
|
|
8 | 1, 3, 5, 7, 9, 11, 13, 15 | |
| 16 | 1, 2, 3, ..., 16 | ||
| 6 | 1, 5, 7, 11, 13, 17 | ||
| 18 | 1, 2, 3, ..., 18 | ||
|
|
8 | 1, 3, 7, 9, 11, 13, 17, 19 | |
|
|
12 | 1, 2, 4, 5, 7, 8, 10, 11, 13, 16, 17, 19 | |
| 10 | 1, 3, 5, 7, 9, 13, 15, 17, 19, 21 | ||
| 22 | 1, 2, 3, ..., 22 | ||
|
|
8 | 1, 5, 7, 11, 13, 17, 19, 23 |
![]() is a Cyclic Group (which occurs exactly when
is a Cyclic Group (which occurs exactly when ![]() has a Primitive Root) Iff
has a Primitive Root) Iff ![]() is of one of the
forms
is of one of the
forms ![]() , 4,
, 4, ![]() , or
, or ![]() , where
, where ![]() is an Odd Prime and
is an Odd Prime and ![]() (Shanks 1993, p. 92).
(Shanks 1993, p. 92).
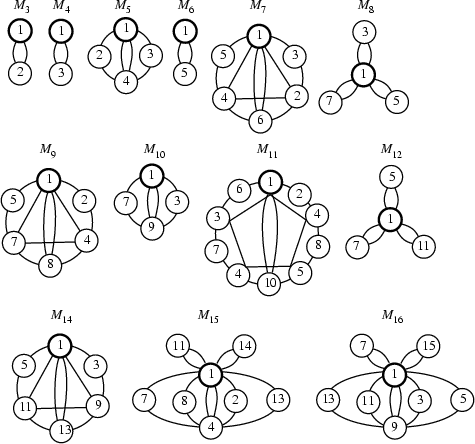
Isomorphic modulo multiplication groups can be determined using a particular type of factorization
of ![]() as described by Shanks (1993, pp. 92-93). To perform this factorization (denoted
as described by Shanks (1993, pp. 92-93). To perform this factorization (denoted ![]() ), factor
), factor ![]() in the
standard form
in the
standard form
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
![]() and
and ![]() are isomorphic Iff
are isomorphic Iff ![]() and
and ![]() are identical. More specifically, the abstract Group
corresponding to a given
are identical. More specifically, the abstract Group
corresponding to a given ![]() can be determined explicitly in terms of a Direct Product of
Cyclic Groups of the so-called Characteristic Factors, whose product
is denoted
can be determined explicitly in terms of a Direct Product of
Cyclic Groups of the so-called Characteristic Factors, whose product
is denoted ![]() . This representation is obtained from
. This representation is obtained from ![]() as the set of products of largest powers of each factor of
as the set of products of largest powers of each factor of
![]() . For example, for
. For example, for ![]() , the largest power of
, the largest power of ![]() is
is ![]() and the largest power of 3 is
and the largest power of 3 is ![]() , so the
first characteristic factor is
, so the
first characteristic factor is ![]() , leaving
, leaving ![]() (i.e., only powers of two). The largest power remaining is
(i.e., only powers of two). The largest power remaining is
![]() , so the second Characteristic Factor is 2, leaving 2, which is the third and last Characteristic Factor.
Therefore,
, so the second Characteristic Factor is 2, leaving 2, which is the third and last Characteristic Factor.
Therefore,
![]() , and the group
, and the group ![]() is isomorphic to
is isomorphic to
![]() .
.
The following table summarizes the isomorphic modulo multiplication groups ![]() for the first few
for the first few ![]() and identifies the
corresponding abstract Group. No
and identifies the
corresponding abstract Group. No ![]() is Isomorphic to
is Isomorphic to ![]() ,
, ![]() , or
, or ![]() . However,
every finite Abelian Group is isomorphic to a Subgroup of
. However,
every finite Abelian Group is isomorphic to a Subgroup of ![]() for infinitely many different values of
for infinitely many different values of ![]() (Shanks 1993, p. 96). Cycle Graphs corresponding to
(Shanks 1993, p. 96). Cycle Graphs corresponding to ![]() for small
for small ![]() are illustrated above, and more
complicated Cycle Graphs are illustrated by Shanks (1993, pp. 87-92).
are illustrated above, and more
complicated Cycle Graphs are illustrated by Shanks (1993, pp. 87-92).
| Group | Isomorphic |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The number of Characteristic Factors ![]() of
of ![]() for
for ![]() , 2, ... are 1, 1, 1, 1, 1, 1,
1, 2, 1, 1, 1, 2, ... (Sloane's A046072). The number of Quadratic Residues in
, 2, ... are 1, 1, 1, 1, 1, 1,
1, 2, 1, 1, 1, 2, ... (Sloane's A046072). The number of Quadratic Residues in ![]() for
for ![]() are
given by
are
given by ![]() (Shanks 1993, p. 95). The first few for
(Shanks 1993, p. 95). The first few for ![]() , 2, ... are 0, 1, 1, 1, 2, 1, 3, 1, 3, 2, 5, 1, 6,
... (Sloane's A046073).
, 2, ... are 0, 1, 1, 1, 2, 1, 3, 1, 3, 2, 5, 1, 6,
... (Sloane's A046073).
In the table below, ![]() is the Totient Function (Sloane's A000010) factored into Characteristic
Factors,
is the Totient Function (Sloane's A000010) factored into Characteristic
Factors, ![]() is the Carmichael Function (Sloane's A011773), and
is the Carmichael Function (Sloane's A011773), and ![]() are the smallest
generators of the group
are the smallest
generators of the group ![]() (of which there is a number equal to the number of Characteristic
Factors).
(of which there is a number equal to the number of Characteristic
Factors).
| 3 | 2 | 2 | 2 | 27 | 18 | 18 | 2 |
| 4 | 2 | 2 | 3 | 28 | 6 | 13, 3 | |
| 5 | 4 | 2 | 2 | 29 | 28 | 28 | 2 |
| 6 | 2 | 2 | 5 | 30 | 4 | 11, 7 | |
| 7 | 6 | 6 | 3 | 31 | 30 | 30 | 3 |
| 8 | 2 | 7, 3 | 32 | 8 | 31, 3 | ||
| 9 | 6 | 6 | 2 | 33 | 10 | 10, 2 | |
| 10 | 4 | 4 | 3 | 34 | 16 | 16 | 3 |
| 11 | 10 | 10 | 2 | 35 | 12 | 6, 2 | |
| 12 | 2 | 5, 7 | 36 | 6 | 19,5 | ||
| 13 | 12 | 12 | 2 | 37 | 36 | 36 | 2 |
| 14 | 6 | 6 | 3 | 38 | 18 | 18 | 3 |
| 15 | 4 | 14, 2 | 39 | 12 | 38, 2 | ||
| 16 | 4 | 15, 3 | 40 |
|
4 | 39, 11, 3 | |
| 17 | 16 | 16 | 3 | 41 | 40 | 40 | 6 |
| 18 | 6 | 6 | 5 | 42 | 6 | 13, 5 | |
| 19 | 18 | 18 | 2 | 43 | 42 | 42 | 3 |
| 20 | 4 | 19, 3 | 44 | 10 | 43, 3 | ||
| 21 | 6 | 20, 2 | 45 | 12 | 44, 2 | ||
| 22 | 10 | 10 | 7 | 46 | 22 | 22 | 5 |
| 23 | 22 | 22 | 5 | 47 | 46 | 46 | 5 |
| 24 |
|
2 | 5, 7, 13 | 48 |
|
4 | 47, 7, 5 |
| 25 | 20 | 20 | 2 | 49 | 42 | 42 | 3 |
| 26 | 12 | 12 | 7 | 50 | 20 | 20 | 3 |
See also Characteristic Factor, Cycle Graph, Finite Group, Residue Class
References
Riesel, H. ``The Structure of the Group
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 61-62 and 92, 1993.
Sloane, N. J. A. Sequences
A011773,
A046072,
A046073, and
A000010/M0299
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
![]() .'' Prime Numbers and Computer Methods for Factorization, 2nd ed.
Boston, MA: Birkhäuser, pp. 270-272, 1994.
.'' Prime Numbers and Computer Methods for Factorization, 2nd ed.
Boston, MA: Birkhäuser, pp. 270-272, 1994.
![]() Weisstein, E. W. ``Groups.'' Mathematica notebook Groups.m.
Weisstein, E. W. ``Groups.'' Mathematica notebook Groups.m.
|
|
|
© 1996-9 Eric W. Weisstein