|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
A Group for which the elements Commute (i.e., ![]() for all elements
for all elements ![]() and
and ![]() ) is
called an Abelian group. All Cyclic Groups are Abelian, but an Abelian group is not necessarily
Cyclic. All Subgroups of an
Abelian group are Normal. In an Abelian group, each element is in a Conjugacy Class by
itself, and the Character Table involves Powers of a single element known as a
Generator.
) is
called an Abelian group. All Cyclic Groups are Abelian, but an Abelian group is not necessarily
Cyclic. All Subgroups of an
Abelian group are Normal. In an Abelian group, each element is in a Conjugacy Class by
itself, and the Character Table involves Powers of a single element known as a
Generator.
No general formula is known for giving the number of nonisomorphic Finite Groups of a given
Order. However, the number of nonisomorphic Abelian Finite Groups ![]() of
any given Order
of
any given Order ![]() is given by writing
is given by writing ![]() as
as
| (1) |
| (2) |
The Kronecker Decomposition Theorem states that every Finite Abelian group can be written as a Direct
Product of Cyclic Groups of Prime Power Orders. If the Orders of a Finite Group is a Prime ![]() , then there exists a single
Abelian group of order
, then there exists a single
Abelian group of order ![]() (denoted
(denoted ![]() ) and no non-Abelian groups. If the Order is a prime squared
) and no non-Abelian groups. If the Order is a prime squared
![]() , then there are two Abelian groups (denoted
, then there are two Abelian groups (denoted ![]() and
and
![]() . If the Order is a
prime cubed
. If the Order is a
prime cubed ![]() , then there are three Abelian groups (denoted
, then there are three Abelian groups (denoted
![]() ,
,
![]() , and
, and
![]() ), and five groups total. If the Order is a Product of two primes
), and five groups total. If the Order is a Product of two primes ![]() and
and ![]() , then
there exists exactly one Abelian group of order
, then
there exists exactly one Abelian group of order ![]() (denoted
(denoted
![]() ).
).
Another interesting result is that if ![]() denotes the number of nonisomorphic Abelian groups of Order
denotes the number of nonisomorphic Abelian groups of Order ![]() , then
, then
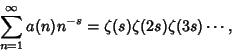 |
(3) |
![\begin{displaymath}
\sum_{n=1}^N a(n)=A_1 N+A_2 N^{1/2}+A_3 N^{1/3}+{\mathcal O}[x^{105/407} (\ln x)^2],
\end{displaymath}](a_129.gif) |
(4) |
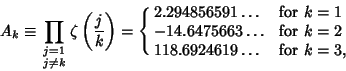 |
(5) |
![\begin{displaymath}
\sum_{n=1}^N {1\over a(n)}=BN+{\mathcal O}[\sqrt{N} (\ln N)^{-1/2}],
\end{displaymath}](a_133.gif) |
(6) |
![\begin{displaymath}
B\equiv \prod\left\{{1-\sum_{k=2}^\infty \left[{{1\over P(k-2)}-{1\over P(k)}}\right]{1\over p^k}}\right\}
= 0.752\ldots
\end{displaymath}](a_134.gif) |
(7) |
See also Finite Group, Group Theory, Kronecker Decomposition Theorem, Partition Function P, Ring
References
DeKoninck, J.-M. and Ivic, A.
Topics in Arithmetical Functions: Asymptotic Formulae for Sums of Reciprocals of Arithmetical Functions and Related Fields.
Amsterdam, Netherlands: North-Holland, 1980.
Erdös, P. and Szekeres, G. ``Über die Anzahl abelscher Gruppen gegebener Ordnung und über ein
verwandtes zahlentheoretisches Problem.'' Acta Sci. Math. (Szeged) 7, 95-102, 1935.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/abel/abel.html
Kendall, D. G. and Rankin, R. A. ``On the Number of Abelian Groups of a Given Order.'' Quart. J. Oxford 18, 197-208, 1947.
Kolesnik, G. ``On the Number of Abelian Groups of a Given Order.'' J. Reine Angew. Math. 329, 164-175, 1981.
Neumann, P. M. ``An Enumeration Theorem for Finite Groups.'' Quart. J. Math. Ser. 2 20, 395-401, 1969.
Pyber, L. ``Enumerating Finite Groups of Given Order.'' Ann. Math. 137, 203-220, 1993.
Richert, H.-E. ``Über die Anzahl abelscher Gruppen gegebener Ordnung I.'' Math. Zeitschr. 56, 21-32, 1952.
Sloane, N. J. A. Sequence
A000688/M0064
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Srinivasan, B. R. ``On the Number of Abelian Groups of a Given Order.'' Acta Arith. 23, 195-205, 1973.
|
|
|
© 1996-9 Eric W. Weisstein