|
|
|
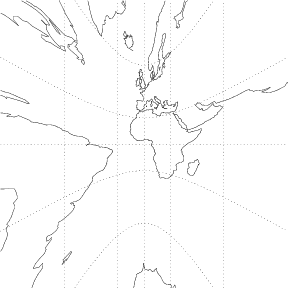
A nonconformal projection from a Sphere's center in which Orthodromes are straight
Lines.
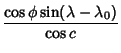 |
(1) | ||
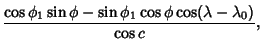 |
(2) |
| (3) |
| (4) | |||
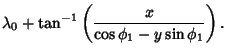 |
(5) |
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 150-153, 1967.
Snyder, J. P. Map Projections--A Working Manual. U. S. Geological Survey Professional Paper 1395.
Washington, DC: U. S. Government Printing Office, pp. 164-168, 1987.