|
|
|
An encoding of numbers so that adjacent numbers have a single Digit differing by 1. A Binary Gray code with ![]() Digits corresponds to a Hamiltonian Path on an
Digits corresponds to a Hamiltonian Path on an ![]() -D Hypercube (including direction reversals).
The term Gray code is often used to refer to a ``reflected'' code, or more specifically still, the binary reflected Gray code.
-D Hypercube (including direction reversals).
The term Gray code is often used to refer to a ``reflected'' code, or more specifically still, the binary reflected Gray code.
To convert a Binary number
![]() to its corresponding binary reflected Gray code, start at the
right with the digit
to its corresponding binary reflected Gray code, start at the
right with the digit ![]() (the
(the ![]() th, or last, Digit). If the
th, or last, Digit). If the ![]() is 1, replace
is 1, replace ![]() by
by ![]() ; otherwise,
leave it unchanged. Then proceed to
; otherwise,
leave it unchanged. Then proceed to ![]() . Continue up to the first Digit
. Continue up to the first Digit ![]() , which is kept the same since
, which is kept the same since
![]() is assumed to be a 0. The resulting number
is assumed to be a 0. The resulting number
![]() is the reflected binary Gray code.
is the reflected binary Gray code.
To convert a binary reflected Gray code
![]() to a Binary number, start again with the
to a Binary number, start again with the ![]() th
digit, and compute
th
digit, and compute
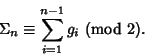
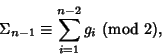
The code is called reflected because it can be generated in the following manner. Take the Gray code 0, 1. Write it forwards, then backwards: 0, 1, 1, 0. Then append 0s to the first half and 1s to the second half: 00, 01, 11, 10. Continuing, write 00, 01, 11, 10, 10, 11, 01, 00 to obtain: 000, 001, 011, 010, 110, 111, 101, 100, ... (Sloane's A014550). Each iteration therefore doubles the number of codes. The Gray codes corresponding to the first few nonnegative integers are given in the following table.
| 0 | 0 | 20 | 11110 | 40 | 111100 |
| 1 | 1 | 21 | 11111 | 41 | 111101 |
| 2 | 11 | 22 | 11101 | 42 | 111111 |
| 3 | 10 | 23 | 11100 | 43 | 111110 |
| 4 | 110 | 24 | 10100 | 44 | 111010 |
| 5 | 111 | 25 | 10101 | 45 | 111011 |
| 6 | 101 | 26 | 10111 | 46 | 111001 |
| 7 | 100 | 27 | 10110 | 47 | 111000 |
| 8 | 1100 | 28 | 10010 | 48 | 101000 |
| 9 | 1101 | 29 | 10011 | 49 | 101001 |
| 10 | 1111 | 30 | 10001 | 50 | 101011 |
| 11 | 1110 | 31 | 10000 | 51 | 101010 |
| 12 | 1010 | 32 | 110000 | 52 | 101110 |
| 13 | 1011 | 33 | 110001 | 53 | 101111 |
| 14 | 1001 | 34 | 110011 | 54 | 101101 |
| 15 | 1000 | 35 | 110010 | 55 | 101100 |
| 16 | 11000 | 36 | 110110 | 56 | 100100 |
| 17 | 11001 | 37 | 110111 | 57 | 100101 |
| 18 | 11011 | 38 | 110101 | 58 | 100111 |
| 19 | 11010 | 39 | 110100 | 59 | 100110 |
The binary reflected Gray code is closely related to the solution of the Towers of Hanoi as well as the Baguenaudier.
See also Baguenaudier, Binary, Hilbert Curve, Ryser Formula, Thue-Morse Sequence, Towers of Hanoi
References
Gardner, M. ``The Binary Gray Code.''
Ch. 2 in Knotted Doughnuts and Other Mathematical Entertainments. New York: W. H. Freeman, 1986.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Gray Codes.'' §20.2 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 886-888, 1992.
Sloane, N. J. A. Sequence
A014550
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Vardi, I. Computational Recreations in Mathematica.
Redwood City, CA: Addison-Wesley, pp. 111-112 and 246, 1991.
|
|
|
© 1996-9 Eric W. Weisstein