The Integer Sequence (also called the Morse-Thue Sequence)
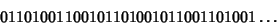 |
(1) |
(Sloane's A010060) which arises in the Thue-Morse Constant. It can be generated from the Substitution Map
starting with 0 as follows:
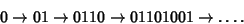 |
(4) |
Writing the sequence as a Power Series over the Galois Field GF(2),
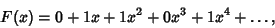 |
(5) |
then 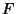 satisfies the quadratic equation
satisfies the quadratic equation
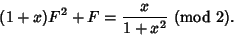 |
(6) |
This equation has two solutions, 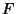 and
and 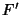 , where
, where 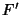 is the complement of
is the complement of 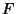 , i.e.,
, i.e.,
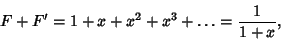 |
(7) |
which is consistent with the formula for the sum of the roots of a quadratic. The equality (6) can be
demonstrated as follows. Let (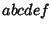 ...) be a shorthand for the Power series
...) be a shorthand for the Power series
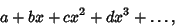 |
(8) |
so 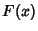 is (0110100110010110...). To get
is (0110100110010110...). To get 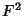 , simply use the rule for
squaring Power Series over GF(2)
, simply use the rule for
squaring Power Series over GF(2)
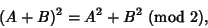 |
(9) |
which extends to the simple rule for squaring a Power Series
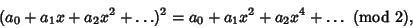 |
(10) |
i.e., space the series out by a factor of 2, (0 1 1 0 1 0 0 1 ...), and insert zeros in the Odd places to get
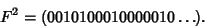 |
(11) |
Then multiply by 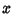 (which just adds a zero at the front) to get
(which just adds a zero at the front) to get
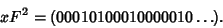 |
(12) |
Adding to 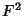 gives
gives
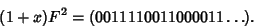 |
(13) |
This is the first term of the quadratic equation, which is the Thue-Morse sequence with each term doubled up. The next
term is 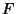 , so we have
, so we have
The sum is the above two sequences XORed together (there are no
Carries because we're working over GF(2)), giving
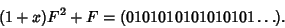 |
(16) |
We therefore have
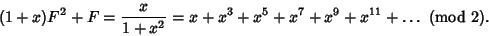 |
(17) |
The Thue-Morse sequence is an example of a cube-free sequence on two symbols (Morse
and Hedlund 1944), i.e., it contains no substrings of the form 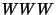 , where
, where  is any
Word. For example, it does not
contain the Words 000, 010101 or 010010010. In fact, the following
stronger statement is true: the Thue-Morse sequence
does not contain any substrings of the form
is any
Word. For example, it does not
contain the Words 000, 010101 or 010010010. In fact, the following
stronger statement is true: the Thue-Morse sequence
does not contain any substrings of the form 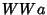 , where
, where 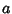 is the first symbol of
is the first symbol of  .
We can obtain a
Squarefree sequence on three symbols by doing the following: take the Thue-Morse sequence 0110100110010110...
and look at the sequence of Words of length 2 that appear: 01 11 10 01 10 00 01 11 10 .... Replace 01 by 0, 10 by 1, 00
by 2 and 11 by 2 to get the following: 021012021.... Then this Sequence is Squarefree (Morse and Hedlund 1944).
.
We can obtain a
Squarefree sequence on three symbols by doing the following: take the Thue-Morse sequence 0110100110010110...
and look at the sequence of Words of length 2 that appear: 01 11 10 01 10 00 01 11 10 .... Replace 01 by 0, 10 by 1, 00
by 2 and 11 by 2 to get the following: 021012021.... Then this Sequence is Squarefree (Morse and Hedlund 1944).
The Thue-Morse sequence has important connections with the Gray Code. Kindermann generates fractal music
using the Self-Similarity of the Thue-Morse sequence.
See also Gray Code, Parity Constant, Rabbit Sequence, Thue Sequence
References
Kindermann, L. ``MusiNum--The Music in the Numbers.''
http://www.forwiss.uni-erlangen.de/~kinderma/musinum/.
Morse, M. and Hedlund, G. A. ``Unending Chess, Symbolic Dynamics, and a Problem in Semigroups.'' Duke
Math. J. 11, 1-7, 1944.
Schroeder, M. R. Fractals, Chaos, and Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, 1991.
Sloane, N. J. A. Sequence
A010060
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , where
, where ![]() is any
Word. For example, it does not
contain the Words 000, 010101 or 010010010. In fact, the following
stronger statement is true: the Thue-Morse sequence
does not contain any substrings of the form
is any
Word. For example, it does not
contain the Words 000, 010101 or 010010010. In fact, the following
stronger statement is true: the Thue-Morse sequence
does not contain any substrings of the form ![]() , where
, where ![]() is the first symbol of
is the first symbol of ![]() .
We can obtain a
Squarefree sequence on three symbols by doing the following: take the Thue-Morse sequence 0110100110010110...
and look at the sequence of Words of length 2 that appear: 01 11 10 01 10 00 01 11 10 .... Replace 01 by 0, 10 by 1, 00
by 2 and 11 by 2 to get the following: 021012021.... Then this Sequence is Squarefree (Morse and Hedlund 1944).
.
We can obtain a
Squarefree sequence on three symbols by doing the following: take the Thue-Morse sequence 0110100110010110...
and look at the sequence of Words of length 2 that appear: 01 11 10 01 10 00 01 11 10 .... Replace 01 by 0, 10 by 1, 00
by 2 and 11 by 2 to get the following: 021012021.... Then this Sequence is Squarefree (Morse and Hedlund 1944).