|
|
|
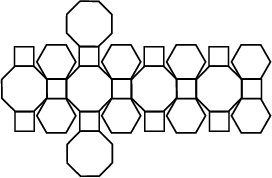
An Archimedean Solid sometimes (improperly) called the Truncated Cuboctahedron and also called the
Rhombitruncated Cuboctahedron. Its Dual is the Disdyakis Dodecahedron, also called the
Hexakis Octahedron. It has Schläfli Symbol t
![]() . It is also
Uniform Polyhedron
. It is also
Uniform Polyhedron ![]() and has Wythoff Symbol
and has Wythoff Symbol ![]() . Its faces are
. Its faces are
![]() . The
Small Cubicuboctahedron is a Faceted version. The Inradius, Midradius, and
Circumradius for unit edge length are
. The
Small Cubicuboctahedron is a Faceted version. The Inradius, Midradius, and
Circumradius for unit edge length are
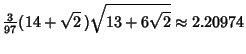 |
|||
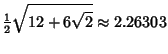 |
|||
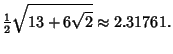 |
See also Small Rhombicuboctahedron, Great Truncated Cuboctahedron
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, p. 138, 1987.