|
|
|
Given Collinear points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ,
, ![]() and
and ![]() are harmonic conjugates with respect to
are harmonic conjugates with respect to ![]() and
and ![]() if
if
Harmonic conjugate points are also defined for a Triangle.
If ![]() and
and ![]() have Trilinear Coordinates
have Trilinear Coordinates
![]() and
and
![]() , then the Trilinear Coordinates of the harmonic conjugates are
, then the Trilinear Coordinates of the harmonic conjugates are
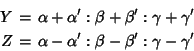
See also Harmonic Range, Harmonic Ratio
References
Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 13-14, 1990.
Phillips, A. W. and Fisher, I. Elements of Geometry. New York: American Book Co., 1896.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. New York: Viking Penguin, p. 92, 1992.