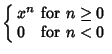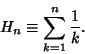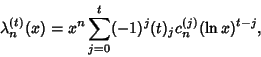For all Integers 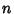 and Nonnegative Integers
and Nonnegative Integers 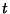 , the harmonic
logarithms
, the harmonic
logarithms
 of order
of order 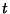 and degree
and degree 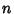 are defined as the unique functions satisfying
are defined as the unique functions satisfying
- 1.
 ,
,
- 2.
 has no constant term except
has no constant term except
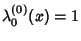 ,
,
- 3.
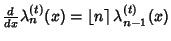 ,
,
where the ``Roman Symbol''
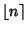 is defined by
is defined by
 |
(1) |
(Roman 1992). This gives the special cases
where 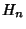 is a Harmonic Number
is a Harmonic Number
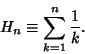 |
(4) |
The harmonic logarithm has the Integral
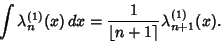 |
(5) |
The harmonic logarithm can be written
 |
(6) |
where 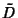 is the Differential Operator, (so
is the Differential Operator, (so 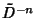 is the
is the 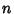 th Integral). Rearranging
gives
th Integral). Rearranging
gives
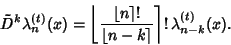 |
(7) |
This formulation gives an analog of the Binomial Theorem called the Logarithmic Binomial Formula.
Another expression for the harmonic logarithm is
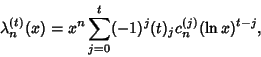 |
(8) |
where
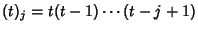 is a Pochhammer Symbol and
is a Pochhammer Symbol and 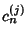 is a two-index Harmonic Number
(Roman 1992).
is a two-index Harmonic Number
(Roman 1992).
See also Logarithm, Roman Factorial
References
Loeb, D. and Rota, G.-C. ``Formal Power Series of Logarithmic Type.'' Advances Math. 75, 1-118, 1989.
Roman, S. ``The Logarithmic Binomial Formula.'' Amer. Math. Monthly 99, 641-648, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and Nonnegative Integers
and Nonnegative Integers ![]() , the harmonic
logarithms
, the harmonic
logarithms
![]() of order
of order ![]() and degree
and degree ![]() are defined as the unique functions satisfying
are defined as the unique functions satisfying