|
|
|
A Quadratic Surface which may be one- or two-sheeted.
The one-sheeted circular hyperboloid
is a doubly Ruled Surface. When oriented along the z-Axis, the one-sheeted circular hyperboloid
has Cartesian Coordinates equation
| (1) |
| (2) | |||
| (3) | |||
| (4) |
| (5) | |||
| (6) | |||
| (7) |
| (8) | |||
| (9) | |||
| (10) |
A two-sheeted circular hyperboloid oriented along the z-Axis has Cartesian Coordinates equation
| (11) |
| (12) | |||
| (13) | |||
| (14) |
| (15) |
| (16) | |||
| (17) | |||
| (18) |
The Support Function of the hyperboloid of one sheet
| (19) |
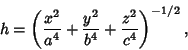 |
(20) |
| (21) |
| (22) |
 |
(23) |
| (24) |
See also Catenoid, Ellipsoid, Elliptic Hyperboloid, Hyperboloid Embedding, Paraboloid, Ruled Surface
References
Fischer, G. (Ed.). Plates 67 and 69 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume.
Braunschweig, Germany: Vieweg, pp. 62 and 64, 1986.
Gray, A. ``The Hyperboloid of Revolution.'' §18.5 in
Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 296-297, 311-314, and 369-370, 1993.
|
|
|
© 1996-9 Eric W. Weisstein