|
|
|
A function
![]() expressed as a double sum of Spherical Harmonics is called a
Laplace series. Taking
expressed as a double sum of Spherical Harmonics is called a
Laplace series. Taking ![]() as a Complex Function,
as a Complex Function,
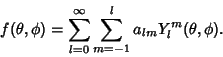 |
(1) |
|
|
|
|
|
|
|
|
(2) |
| (3) |
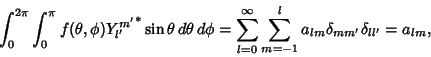 |
(4) |
For a Real series, consider
![\begin{displaymath}
f(\theta,\phi) = \sum_{l=0}^\infty\sum_{m=-1}^l [C_l^m\cos(m\phi)+S_l^m\sin(m\phi)] P_l^m(\cos\theta).
\end{displaymath}](l1_658.gif) |
(5) |
|
|
|
|
|
(6) |
|
|
|
|
|
(7) |
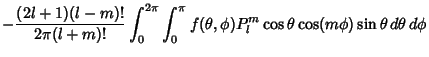 |
(8) | ||
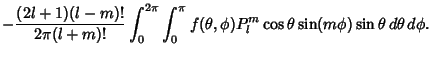 |
(9) |