N.B. A detailed on-line essay by S. Finch
was the starting point for this entry.
Assume a function 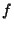 is integrable over the interval
is integrable over the interval ![$[-\pi, \pi]$](l1_1152.gif) and
and 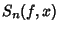 is the
is the 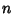 th partial sum of the
Fourier Series of
th partial sum of the
Fourier Series of 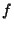 , so that
, so that
and
![\begin{displaymath}
S_n(f,x)={\textstyle{1\over 2}}a_0+\left\{{\sum_{k=1}^n [a_k\cos(kx)+b_k\sin(kx)]}\right\}.
\end{displaymath}](l1_1158.gif) |
(3) |
If
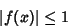 |
(4) |
for all 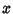 , then
, then
![\begin{displaymath}
S_n(f,x)\leq {1\over\pi}\int_0^\pi {\vert\sin[{\textstyle{1\...
...ta]\vert\over\sin({\textstyle{1\over 2}}\theta)}\,d\theta=L_n,
\end{displaymath}](l1_1160.gif) |
(5) |
and 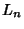 is the smallest possible constant for which this holds for all continuous
is the smallest possible constant for which this holds for all continuous 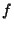 . The first few values of
. The first few values of 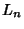 are
are
Some Formulas for 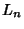 include
include
(Zygmund 1959) and integral Formulas include
(Hardy 1942). For large 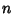 ,
,
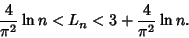 |
(12) |
This result can be generalized for an 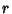 -differentiable function satisfying
-differentiable function satisfying
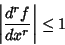 |
(13) |
for all 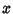 . In this case,
. In this case,
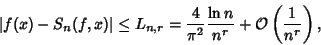 |
(14) |
where
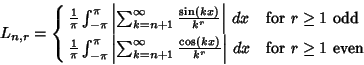 |
(15) |
(Kolmogorov 1935, Zygmund 1959).
Watson (1930) showed that
![\begin{displaymath}
\lim_{n\to\infty} \left[{L_n-{4\over\pi^2}\ln(2n+1)}\right]=c,
\end{displaymath}](l1_1175.gif) |
(16) |
where
where 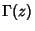 is the Gamma Function,
is the Gamma Function, 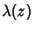 is the Dirichlet Lambda Function, and
is the Dirichlet Lambda Function, and 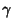 is the
Euler-Mascheroni Constant.
is the
Euler-Mascheroni Constant.
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lbsg/lbsg.html
Hardy, G. H. ``Note on Lebesgue's Constants in the Theory of Fourier Series.'' J. London Math. Soc. 17, 4-13, 1942.
Kolmogorov, A. N. ``Zur Grössenordnung des Restgliedes Fourierscher reihen differenzierbarer Funktionen.''
Ann. Math. 36, 521-526, 1935.
Watson, G. N. ``The Constants of Landau and Lebesgue.'' Quart. J. Math. Oxford 1, 310-318, 1930.
Zygmund, A. G. Trigonometric Series, 2nd ed., Vols. 1-2. Cambridge, England: Cambridge University Press, 1959.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is integrable over the interval
is integrable over the interval ![]() and
and ![]() is the
is the ![]() th partial sum of the
Fourier Series of
th partial sum of the
Fourier Series of ![]() , so that
, so that
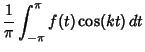
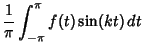
![\begin{displaymath}
S_n(f,x)={\textstyle{1\over 2}}a_0+\left\{{\sum_{k=1}^n [a_k\cos(kx)+b_k\sin(kx)]}\right\}.
\end{displaymath}](l1_1158.gif)
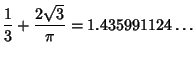
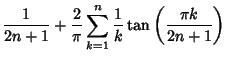
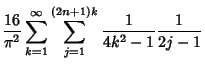
![$\displaystyle 4\int_0^\infty {\tanh[(2n+1)x]\over\tanh x} {dx\over \pi^2+4x^2}$](l1_1169.gif)
![$\displaystyle {4\over\pi^2} \int_0^\infty {\sinh[(2n+1)x]\over\sinh x} \ln\{\coth[{\textstyle{1\over 2}}(2n+1)x]\}\,dx$](l1_1170.gif)
![]() -differentiable function satisfying
-differentiable function satisfying
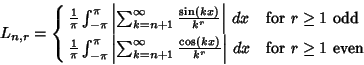
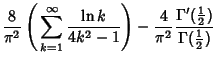
![$\displaystyle {8\over \pi^2}\left[{\,\sum_{j=0}^\infty {\lambda(2j+2)-1\over 2j+1}}\right]+{4\over\pi^2} (2\ln 2+\gamma)$](l1_1177.gif)