Magic Cube

An $n\times n\times n$ 3-D version of the Magic Square in which the $n^2$ rows, $n^2$ columns, $n^2$ pillars (or ``files''), and four space diagonals each sum to a single number $M_3(n)$ known as the Magic Constant. If the cross-section diagonals also sum to $M_3(n)$, the magic cube is called a Perfect Magic Cube; if they do not, the cube is called a Semiperfect Magic Cube, or sometimes an Andrews Cube (Gardner 1988). A pandiagonal cube is a perfect or semiperfect magic cube which is magic not only along the main space diagonals, but also on the broken space diagonals.

A magic cube using the numbers 1, 2, ..., $n^3$, if it exists, has Magic Constant

$$M_3(n)={1\over n^2}\sum_{k=1}^{n^3} k = {\textstyle{1\over 2}}n(n^3+1) = {\textstyle{1\over 2}}n(n+1)(n^2-n+1).$$

For $n=1$, 2, ..., the magic constants are 1, 9, 42, 130, 315, 651, ... (Sloane's A027441).

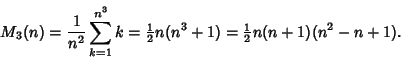
The above semiperfect magic cubes of orders three (Hunter and Madachy 1975, p. 31; Ball and Coxeter 1987, p. 218) and four (Ball and Coxeter 1987, p. 220) have magic constants 42 and 130, respectively. There is a trivial semiperfect magic cube of order one, but no semiperfect cubes of orders two or three exist. Semiperfect cubes of Odd order with $n\geq 5$ and Doubly Even order can be constructed by extending the methods used for Magic Squares.

There are no perfect magic cubes of order four (Beeler et al. 1972, Item 50; Gardner 1988). No perfect magic cubes of order five are known, although it is known that such a cube must have a central value of 63 (Beeler et al. 1972, Item 51; Gardner 1988). No order-six perfect magic cubes are known, but Langman (1962) constructed a perfect magic cube of order seven. An order-eight perfect magic cube was published anonymously in 1875 (Barnard 1888, Benson and Jacoby 1981, Gardner 1988). The construction of such a cube is discussed in Ball and Coxeter (1987). Rosser and Walker rediscovered the order-eight cube in the late 1930s (but did not publish it), and Myers independently discovered the cube illustrated above in 1970 (Gardner 1988). Order 9 and 11 magic cubes have also been discovered, but none of order 10 (Gardner 1988).

Semiperfect pandiagonal cubes exist for all orders $8n$ and all Odd $n>8$ (Ball and Coxeter 1987). A perfect pandiagonal magic cube has been constructed by Planck (1950), cited in Gardner (1988).

Berlekamp et al. (1982, p. 783) give a magic Tesseract.

See also Magic Constant, Magic Graph, Magic Hexagon, Magic Square

References

Adler, A. and Li, S.-Y. R. ``Magic Cubes and Prouhet Sequences.'' Amer. Math. Monthly 84, 618-627, 1977.

Andrews, W. S. Magic Squares and Cubes, 2nd rev. ed. New York: Dover, 1960.

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 216-224, 1987.

Barnard, F. A. P. ``Theory of Magic Squares and Cubes.'' Mem. Nat. Acad. Sci. 4, 209-270, 1888.

Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.

Benson, W. H. and Jacoby, O. Magic Cubes: New Recreations. New York: Dover, 1981.

Berlekamp, E. R.; Conway, J. H; and Guy, R. K. Winning Ways, For Your Mathematical Plays, Vol. 2: Games in Particular. London: Academic Press, 1982.

Gardner, M. ``Magic Squares and Cubes.'' Ch. 17 in Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 213-225, 1988.

Hendricks, J. R. ``Ten Magic Tesseracts of Order Three.'' J. Recr. Math. 18, 125-134, 1985-1986.

Hirayama, A. and Abe, G. Researches in Magic Squares. Osaka, Japan: Osaka Kyoikutosho, 1983.

Hunter, J. A. H. and Madachy, J. S. ``Mystic Arrays.'' Ch. 3 in Mathematical Diversions. New York: Dover, p. 31, 1975.

Langman, H. Play Mathematics. New York: Hafner, pp. 75-76, 1962.

Lei, A. ``Magic Cube and Hypercube.'' http://www.cs.ust.hk/~philipl/magic/mcube2.html.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 99-100, 1979.

Pappas, T. ``A Magic Cube.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 77, 1989.

Planck, C. Theory of Path Nasiks. Rugby, England: Privately Published, 1905.

Rosser, J. B. and Walker, R. J. ``The Algebraic Theory of Diabolical Squares.'' Duke Math. J. 5, 705-728, 1939.

Sloane, N. J. A. Sequence A027441 in ``The On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html.

Wynne, B. E. ``Perfect Magic Cubes of Order 7.'' J. Recr. Math. 8, 285-293, 1975-1976.