|
|
|
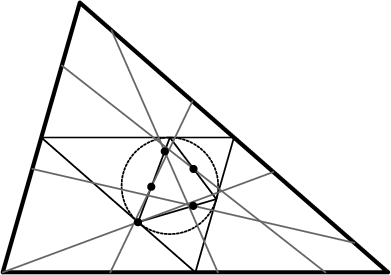
Given an original triangle (thick line), find the Medial Triangle (outer thin line) and its Incircle. Take the
Pedal Triangle (inner thin line) of the Medial Triangle with the Incenter as the Pedal Point. Now
pick any point on the original triangle, and connect it to the point located a half-Perimeter away (gray lines). Then
the locus of the Midpoints of these lines (the ![]() s in the above diagram) is the Pedal
Triangle.
s in the above diagram) is the Pedal
Triangle.
References
Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 261-267, 1991.
Tsintsifas, G. ``Problem 674.'' Crux Math., p. 256, 1982.