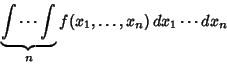A repeated integral over  variables
variables
is called a multiple integral. An 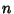 th order integral corresponds, in general, to an
th order integral corresponds, in general, to an 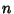 -D Volume (Content),
with
-D Volume (Content),
with 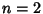 corresponding to an Area. In an indefinite multiple integral, the order in which the integrals are carried
out can be varied at will; for definite multiple integrals, care must be taken to correctly transform the limits if the order
is changed.
corresponding to an Area. In an indefinite multiple integral, the order in which the integrals are carried
out can be varied at will; for definite multiple integrals, care must be taken to correctly transform the limits if the order
is changed.
See also Integral, Monte Carlo Integration
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Multidimensional Integrals.'' §4.6 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 155-158, 1992.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() variables
variables