|
|
|
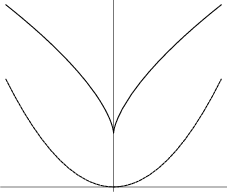
The solid curve in the above figure which is the Evolute of the Parabola (dashed curve). In Cartesian
Coordinates,
See also Parabola Evolute
References
Lee, X. ``Semicubic Parabola.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/SemicubicParabola_dir/semicubicParabola.html
MacTutor History of Mathematics Archive. ``Neile's Semi-Cubical Parabola.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Neiles.html.