Panmagic Square

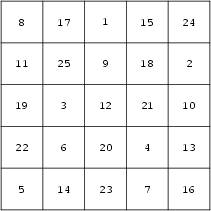
If all the diagonals (including those obtained by ``wrapping around'' the edges) of a Magic Square, as well as the usual rows, columns, and main diagonals sum to the Magic Constant, the square is said to be a Panmagic Square (also called Diabolical Square, Nasik Square, or Pandiagonal Square). No panmagic squares exist of order 3 or any order $4k+2$ for $k$ an Integer. The Siamese method for generating Magic Squares produces panmagic squares for orders $6k\pm 1$ with ordinary vector (2, 1) and break vector (1, $-1$).

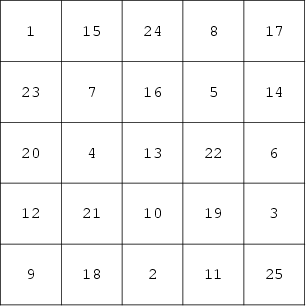
The Lo Shu is not panmagic, but it is an Associative Magic Square. Order four squares can be panmagic or Associative, but not both. Order five squares are the smallest which can be both Associative and panmagic, and 16 distinct Associative panmagic squares exist, one of which is illustrated above (Gardner 1988).

The number of distinct panmagic squares of order 1, 2, ... are 1, 0, 0, 384, 3600, 0, ... (Sloane's A027567, Hunter and Madachy 1975). Panmagic squares are related to Hypercubes.

See also Associative Magic Square, Hypercube, Franklin Magic Square, Magic Square

References

Gardner, M. The Second Scientific American Book of Mathematical Puzzles & Diversions: A New Selection. New York: Simon and Schuster, pp. 135-137, 1961.

Gardner, M. ``Magic Squares and Cubes.'' Ch. 17 in Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 213-225, 1988.

Hunter, J. A. H. and Madachy, J. S. ``Mystic Arrays.'' Ch. 3 in Mathematical Diversions. New York: Dover, pp. 24-25, 1975.

Kraitchik, M. ``Panmagic Squares.'' §7.9 in Mathematical Recreations. New York: W. W. Norton, pp. 174-176, 1942.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 87, 1979.

Rosser, J. B. and Walker, R. J. ``The Algebraic Theory of Diabolical Squares.'' Duke Math. J. 5, 705-728, 1939.

Sloane, N. J. A. Sequence A027567 in ``The On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html.