The Arc Length of the parabolic segment shown above is given by
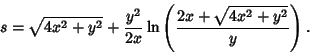 |
(1) |
The Area contained between the curves
can be found by eliminating 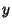 ,
,
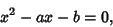 |
(4) |
so the points of intersection are
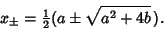 |
(5) |
Therefore, for the Area to be Nonnegative, 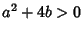 , and
, and
so the Area is
Now,
So
We now wish to find the maximum Area of an inscribed Triangle. This Triangle will have two of its
Vertices at the intersections, and Area
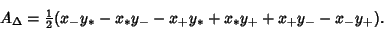 |
(11) |
But 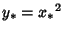 , so
, so
The maximum Area will occur when
![\begin{displaymath}
{\partial A_\Delta\over \partial x_*} = {\textstyle{1\over 2}}[-2(x_+-x_-)x_*+(y_+-y_-)]=0.
\end{displaymath}](p1_504.gif) |
(13) |
But
so
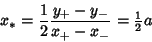 |
(16) |
and
![\begin{displaymath}
A_\Delta = {\textstyle{1\over 2}}[-({\textstyle{1\over 2}}a)^2(x_+-x_-)+({\textstyle{1\over 2}}a)(y_+-y_-)+(x_+y_--x_-y_+)].
\end{displaymath}](p1_510.gif) |
(17) |
Working on the third term
so
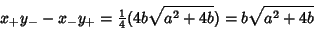 |
(20) |
and
which gives the result known to Archimedes  in the third century BC
in the third century BC  that
that
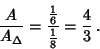 |
(22) |
The Area of the parabolic segment of height 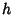 opening upward along the y-Axis is
opening upward along the y-Axis is
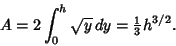 |
(23) |
The weighted mean of 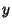 is
is
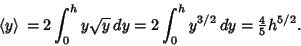 |
(24) |
The Centroid is then given by
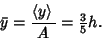 |
(25) |
See also Centroid (Geometric), Parabola, Segment
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 125, 1987.
© 1996-9 Eric W. Weisstein
1999-05-26
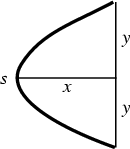
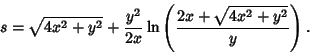
![$\displaystyle \int_{x_-}^{x_+} [(ax+b)-x^2]\,dx$](p1_486.gif)
![]() opening upward along the y-Axis is
opening upward along the y-Axis is