A Tensor sometimes known as the Riemann-Christoffel Tensor. Let
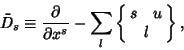 |
(1) |
where the quantity inside the
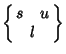 is a
Christoffel Symbol of the Second Kind. Then
is a
Christoffel Symbol of the Second Kind. Then
 |
(2) |
Broken down into its simplest decomposition in  -D,
-D,

|
|
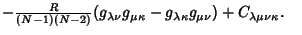
|
(3) |
Here, 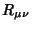 is the Ricci Tensor,
is the Ricci Tensor, 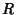 is the Curvature Scalar, and
is the Curvature Scalar, and
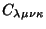 is the
Weyl Tensor. In terms of the Jacobi Tensor
is the
Weyl Tensor. In terms of the Jacobi Tensor
 ,
,
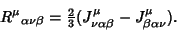 |
(4) |
The Riemann tensor is the only tensor that can be constructed from the Metric Tensor and its first and second
derivatives,
 |
(5) |
where  are Connection Coefficients and
are Connection Coefficients and 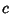 are Commutation
Coefficients. The number of independent coordinates in
are Commutation
Coefficients. The number of independent coordinates in 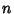 -D is
-D is
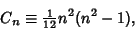 |
(6) |
and the number of Scalars which can be constructed from
 and
and 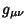 is
is
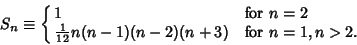 |
(7) |
In 1-D,  .
.
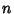 |
 |
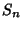 |
| 1 |
0 |
0 |
| 2 |
1 |
1 |
| 3 |
6 |
3 |
| 4 |
20 |
14 |
See also Bianchi Identities, Christoffel Symbol of the Second Kind, Commutation Coefficient,
Connection Coefficient, Curvature Scalar, Gaussian Curvature, Jacobi Tensor, Petrov
Notation, Ricci Tensor, Weyl Tensor
© 1996-9 Eric W. Weisstein
1999-05-25
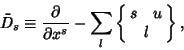
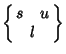 is a
Christoffel Symbol of the Second Kind. Then
is a
Christoffel Symbol of the Second Kind. Then