A Partial Differential Equation which appears in differential geometry and relativistic field theory. Its name is
a pun on its similar form to the Klein-Gordon Equation. The sine-Gordon equation is
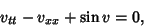 |
(1) |
where  and
and 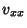 are Partial Derivatives.
The equation can be transformed by defining
are Partial Derivatives.
The equation can be transformed by defining
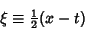 |
(2) |
 |
(3) |
giving
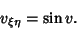 |
(4) |
Traveling wave analysis gives
![\begin{displaymath}
z-z_0=\sqrt{c^2-1} \int{df \over \sqrt{2[d-2\sin^2({\textstyle{1\over 2}}f)]}}.
\end{displaymath}](s1_1474.gif) |
(5) |
For  ,
,
![\begin{displaymath}
z-z_0=\pm\sqrt{1-c^2}\,\ln[\pm \tan({\textstyle{1\over 4}}f)]
\end{displaymath}](s1_1476.gif) |
(6) |
![\begin{displaymath}
f(z)= \pm 4\tan^{-1} [e^{\pm (z-z_0)/(1-c^2)^{1/2}}].
\end{displaymath}](s1_1477.gif) |
(7) |
Letting
 then gives
then gives
 |
(8) |
Letting
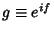 gives
gives
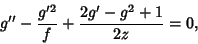 |
(9) |
which is the third Painlevé Transcendent. Look for a solution of the form
![\begin{displaymath}
v(x,t)=4\tan^{-1}\left[{\phi(x)\over \psi(t)}\right].
\end{displaymath}](s1_1482.gif) |
(10) |
Taking the partial derivatives gives
which can be solved in terms of Elliptic Functions. A single Soliton solution
exists with 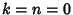 ,
,  :
:
![\begin{displaymath}
v=4\tan^{-1}\left[{\mathop{\rm exp}\nolimits \left({\pm x-\beta t\over \sqrt{1-\beta^2}}\right)}\right],
\end{displaymath}](s1_1489.gif) |
(13) |
where
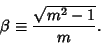 |
(14) |
A two-Soliton solution exists with 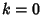 ,
,  :
:
![\begin{displaymath}
v=4\tan^{-1}\left[{\sinh(\beta mx)\over \beta\cosh(\beta mt)}\right].
\end{displaymath}](s1_1491.gif) |
(15) |
A Soliton-antisoliton solution exists with 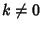 ,
,
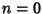 ,
,  :
:
![\begin{displaymath}
v=-4\tan^{-1}\left[{\sinh(\beta mx)\over\beta\cosh(mt)}\right].
\end{displaymath}](s1_1495.gif) |
(16) |
A ``breather'' solution is
![\begin{displaymath}
v=-4\tan^{-1}\left[{{m\over\sqrt{1-m^2}} {\sin(\sqrt{1-m^2t}\,)\over\cosh(mx)}}\right].
\end{displaymath}](s1_1496.gif) |
(17) |
References
Infeld, E. and Rowlands, G. Nonlinear Waves, Solitons, and Chaos. Cambridge, England:
Cambridge University Press, pp. 199-200, 1990.
© 1996-9 Eric W. Weisstein
1999-05-26
![\begin{displaymath}
z-z_0=\sqrt{c^2-1} \int{df \over \sqrt{2[d-2\sin^2({\textstyle{1\over 2}}f)]}}.
\end{displaymath}](s1_1474.gif)
![\begin{displaymath}
v=4\tan^{-1}\left[{\mathop{\rm exp}\nolimits \left({\pm x-\beta t\over \sqrt{1-\beta^2}}\right)}\right],
\end{displaymath}](s1_1489.gif)
![\begin{displaymath}
v=-4\tan^{-1}\left[{{m\over\sqrt{1-m^2}} {\sin(\sqrt{1-m^2t}\,)\over\cosh(mx)}}\right].
\end{displaymath}](s1_1496.gif)