|
|
|
Smarandache sequences are any of a number of simply generated Integer Sequences resembling those considered in published works by Smarandache such as the Consecutive Number Sequences and Euclid Numbers (Iacobescu 1997). Other Smarandache-type sequences are given below.
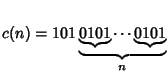 for
for
See also Addition Chain, Consecutive Number Sequences, Cubic Number, Euclid Number, Even Number, Fibonacci Number, Integer Sequence, Odd Number, Partition, Smarandache Function, Square Number
References
Aschbacher, C. Collection of Problems On Smarandache Notions. Vail, AZ: Erhus University Press, 1996.
Aschbacher, C. and Mudge, M. Personal Computer World. pp. 302, Oct. 1995.
Begay, A. ``Smarandache Ceil Functions.'' Bull. Pure Appl. Sci. 16E, 227-229, 1997.
Bencze, M. ``Smarandache Recurrence Type Sequences.'' Bull. Pure Appl. Sci. 16E, 231-236, 1997.
Bencze, M. and Tutescu, L. (Eds.). Some Notions and Questions in Number Theory, Vol. 2.
http://www.gallup.unm.edu/~smarandache/SNAQINT2.TXT.
Brown, J. ``Crescendo & Descrescendo.'' In Richard Henry Wilde: An Anthology in Memoriam (1789-1847) (Ed. M. Myers).
Bristol, IN: Bristol Banner Books, p. 19, 1997.
Brown, J. and Castillo, J. ``Problem 4619.'' School Sci. Math. 97, 221-222, 1997.
Dumitrescu, C. and Seleacu, V. (Ed.). Some Notions and Questions in Number Theory, 4th ed.
Glendale, AZ: Erhus University Press, 1994.
http://www.gallup.unm.edu/~smarandache/SNAQINT.TXT.
Dumitrescu, C. and Seleacu, V. (Ed.).
Proceedings of the First International Conference on Smarandache Type Notions in Number Theory.
Lupton, AZ: American Research Press, 1997.
Hamel, E. Solution to Problem 4619. School Sci. Math. 97, 221-222, 1997.
Iacobescu, F. ``Smarandache Partition Type and Other Sequences.'' Bull. Pure Appl. Sci. 16E, 237-240, 1997.
Ibstedt, H. Surfing on the Ocean of Numbers--A Few Smarandache Notions and Similar Topics.
Lupton, AZ: Erhus University Press, 1997.
Kashihara, K. Comments and Topics on Smarandache Notions and Problems.ail, AZ: Erhus University Press, 1996.
Mudge, M. ``Top of the Class.'' Personal Computer World, 674-675, June 1995.
Mudge, M. ``Not Numerology but Numeralogy!'' Personal Computer World, 279-280, 1997.
Programs and the Abstracts of the First International Conference on Smarandache Notions in Number Theory. Craiova, Romania, Aug. 21-23, 1997.
Radu, I. M. Mathematical Spectrum 27, 43, 1994/1995.
Sloane, N. J. A. Sequences A000452, A000461, A000462, A001156/M0221, A002260, A003108/M0209, A003278/M0975,
A004736, A004737, A004738, A004739, A004741, A007907,
A008318, A008319, A008320, A0083201, A008322,
A015047, A015048,
A019524, A019511, A019513, A019514, A019515, A019516, A019523, A019544, A019545, A019546
A020549,
A031974, A031976, A031980, A031981, A031982,
A046030, A046031, and A046034 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Smarandache, F. ``Properties of the Numbers.'' Tempe, AZ: Arizona State University Special Collection, 1975.
Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.
Smarandache, F. Collected Papers, Vol. 2. Kishinev, Moldova: Kishinev University Press, 1997.
Smith, S. ``A Set of Conjectures on Smarandache Sequences.'' Bull. Pure Appl. Sci. 15E, 101-107, 1996.
|
|
|
© 1996-9 Eric W. Weisstein