If 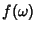 is Square Integrable over the Real
is Square Integrable over the Real 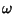 axis, then any one of
the following implies the other two:
axis, then any one of
the following implies the other two:
- 1. The Fourier Transform of
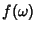 is 0 for
is 0 for 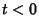 .
.
- 2. Replacing
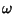 by
by 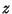 , the function
, the function  is analytic in the Complex Plane
is analytic in the Complex Plane 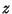 for
for 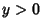 and
approaches
and
approaches  almost everywhere as
almost everywhere as 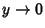 . Furthermore,
. Furthermore,
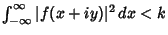 for some number
for some number 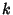 and
and 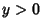 (i.e., the integral is bounded).
(i.e., the integral is bounded).
- 3. The Real and Imaginary Parts of
 are Hilbert
Transforms of each other.
are Hilbert
Transforms of each other.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is Square Integrable over the Real
is Square Integrable over the Real ![]() axis, then any one of
the following implies the other two:
axis, then any one of
the following implies the other two: