|
|
|
An Artin ![]() -function over the Rationals
-function over the Rationals ![]() encodes in a Generating Function
information about how an irreducible monic Polynomial over
encodes in a Generating Function
information about how an irreducible monic Polynomial over ![]() factors when reduced modulo each Prime. For
the Polynomial
factors when reduced modulo each Prime. For
the Polynomial ![]() , the Artin
, the Artin ![]() -function is
-function is
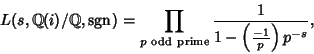
See also Langlands Reciprocity
References
Knapp, A. W. ``Group Representations and Harmonic Analysis, Part II.'' Not. Amer. Math. Soc. 43, 537-549, 1996.