|
|
|
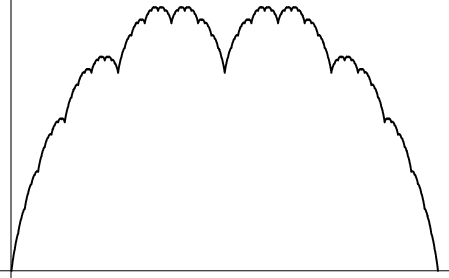
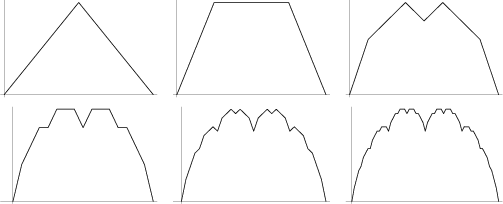
A Continuous Function which is nowhere Differentiable. The iterations towards the continuous function are
Batrachions resembling the Hofstadter-Conway $10,000 Sequence. The first six iterations are
illustrated below. The ![]() th iteration contains
th iteration contains ![]() points, where
points, where ![]() , and can be obtained by setting
, and can be obtained by setting
![]() , letting
, letting
Peitgen and Saupe (1988) refer to this curve as the Takagi Fractal Curve.
See also Hofstadter-Conway $10,000 Sequence, Weierstraß Function
References
Dixon, R. Mathographics. New York: Dover, pp. 175-176 and 210, 1991.
Peitgen, H.-O. and Saupe, D. (Eds.). ``Midpoint Displacement and Systematic Fractals: The Takagi Fractal Curve, Its Kin, and the Related
Systems.'' §A.1.2 in The Science of Fractal Images. New York: Springer-Verlag, pp. 246-248, 1988.
Takagi, T. ``A Simple Example of the Continuous Function without Derivative.'' Proc. Phys. Math. Japan 1, 176-177, 1903.
Tall, D. O. ``The Blancmange Function, Continuous Everywhere but Differentiable Nowhere.'' Math. Gaz. 66, 11-22, 1982.
Tall, D. ``The Gradient of a Graph.'' Math. Teaching 111, 48-52, 1985.