|
|
|
A problem originating with W. Burnside (1902), who wrote, ``A still undecided point in the theory of discontinuous groups is whether the Order of a Group may be not finite, while the order of every operation it contains is finite.'' This question would now be phrased as ``Can a finitely generated group be infinite while every element in the group has finite order?'' (Vaughan-Lee 1990). This question was answered by Golod (1964) when he constructed finitely generated infinite p-Group. These Groups, however, do not have a finite exponent.
Let ![]() be the Free Group of Rank
be the Free Group of Rank ![]() and let
and let ![]() be the Subgroup generated by the set of
be the Subgroup generated by the set of
![]() th Powers
th Powers
![]() . Then
. Then ![]() is a normal subgroup of
is a normal subgroup of ![]() . We define
. We define
![]() to be
the Quotient Group. We call
to be
the Quotient Group. We call ![]() the
the ![]() -generator Burnside group of exponent
-generator Burnside group of exponent ![]() . It is the largest
. It is the largest ![]() -generator
group of exponent
-generator
group of exponent ![]() , in the sense that every other such group is a Homeomorphic image of
, in the sense that every other such group is a Homeomorphic image of ![]() . The Burnside problem
is usually stated as: ``For which values of
. The Burnside problem
is usually stated as: ``For which values of ![]() and
and ![]() is
is ![]() a Finite Group?''
a Finite Group?''
An answer is known for the following values. For ![]() ,
, ![]() is a Cyclic Group of Order
is a Cyclic Group of Order
![]() . For
. For ![]() ,
, ![]() is an elementary Abelian 2-group of Order
is an elementary Abelian 2-group of Order ![]() . For
. For
![]() ,
, ![]() was proved to be finite by Burnside. The Order of the
was proved to be finite by Burnside. The Order of the ![]() groups was established
by Levi and van der Waerden (1933), namely
groups was established
by Levi and van der Waerden (1933), namely ![]() where
where
| (1) |
| (2) | |||
| (3) | |||
| (4) | |||
| (5) |
| (6) | |||
| (7) | |||
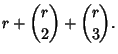 |
(8) |
E. Zelmanov was awarded a Fields Medal in 1994 for his solution of the ``restricted'' Burnside problem.
See also Free Group
References
Burnside, W. ``On an Unsettled Question in the Theory of Discontinuous Groups.'' Quart. J. Pure Appl. Math.
33, 230-238, 1902.
Golod, E. S. ``On Nil-Algebras and Residually Finite
Hall, M. ``Solution of the Burnside Problem for Exponent Six.'' Ill. J. Math. 2, 764-786, 1958.
Levi, F. and van der Waerden, B. L. ``Über eine besondere Klasse von Gruppen.''
Abh. Math. Sem. Univ. Hamburg 9, 154-158, 1933.
Novikov, P. S. and Adjan, S. I. ``Infinite Periodic Groups I, II, III.'' Izv. Akad. Nauk SSSR Ser. Mat.
32, 212-244, 251-524, and 709-731, 1968.
Sanov, I. N. ``Solution of Burnside's problem for exponent four.'' Leningrad State Univ. Ann. Math. Ser.
10, 166-170, 1940.
Vaughan-Lee, M. The Restricted Burnside Problem, 2nd ed. New York: Clarendon Press, 1993.
![]() -Groups.'' Isv. Akad. Nauk SSSR Ser. Mat.
28, 273-276, 1964.
-Groups.'' Isv. Akad. Nauk SSSR Ser. Mat.
28, 273-276, 1964.
|
|
|
© 1996-9 Eric W. Weisstein