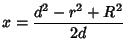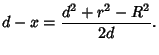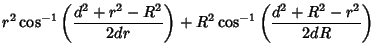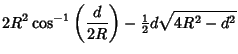Let two Circles of Radii 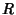 and
and  and centered at
and centered at 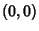 and
and 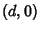 intersect
in a Lens-shaped region. The equations of the two circles are
intersect
in a Lens-shaped region. The equations of the two circles are
Combining (1) and (2) gives
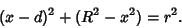 |
(3) |
Multiplying through and rearranging gives
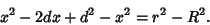 |
(4) |
Solving for  results in
results in
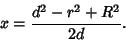 |
(5) |
The line connecting the cusps of the Lens therefore has half-length given by plugging  back in to obtain
back in to obtain
giving a length of
This same formulation applies directly to the Sphere-Sphere Intersection problem.
To find the Area of the asymmetric ``Lens'' in which the Circles intersect,
simply use the formula for the circular Segment of radius 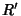 and triangular height
and triangular height 
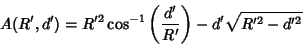 |
(8) |
twice, one for each half of the ``Lens.'' Noting that the heights of the two segment triangles are
The result is
The limiting cases of this expression can be checked to give 0 when 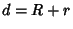 and
and
when  , as expected. In order for half the area of two Unit Disks (
, as expected. In order for half the area of two Unit Disks (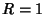 ) to overlap, set
) to overlap, set
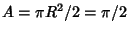 in the above equation
in the above equation
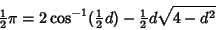 |
(14) |
and solve numerically, yielding
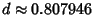 .
.
See also Lens, Segment, Sphere-Sphere Intersection
© 1996-9 Eric W. Weisstein
1999-05-26
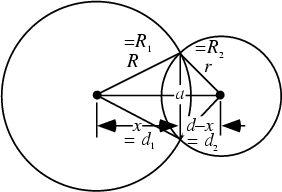
![]() and
and ![]() and centered at
and centered at ![]() and
and ![]() intersect
in a Lens-shaped region. The equations of the two circles are
intersect
in a Lens-shaped region. The equations of the two circles are
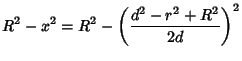
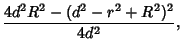
![]() and triangular height
and triangular height ![]()