|
|
|
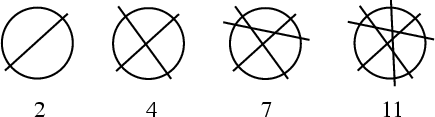
Determining the maximum number of pieces in which it is possible to divide a Circle for a given number of cuts is
called the circle cutting, or sometimes Pancake Cutting, problem. The minimum number is always ![]() , where
, where ![]() is the
number of cuts, and it is always possible to obtain any number of pieces between the minimum and maximum. The first cut
creates 2 regions, and the
is the
number of cuts, and it is always possible to obtain any number of pieces between the minimum and maximum. The first cut
creates 2 regions, and the ![]() th cut creates
th cut creates ![]() new regions, so
new regions, so
| (1) | |||
| (2) | |||
| (3) |
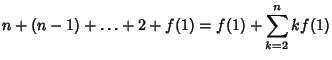 |
|||
| (4) |
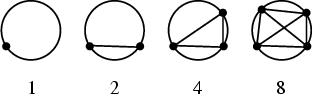
A related problem, sometimes called Moser's Circle Problem, is to find the number of pieces into which a Circle
is divided if ![]() points on its Circumference are joined by Chords with no three Concurrent.
The answer is
points on its Circumference are joined by Chords with no three Concurrent.
The answer is
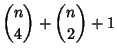 |
(5) | ||
| (6) |
See also Cake Cutting, Cylinder Cutting, Ham Sandwich Theorem, Pancake Theorem, Pizza Theorem, Square Cutting, Torus Cutting
References
Conway, J. H. and Guy, R. K. ``How Many Regions.'' In The Book of Numbers. New York:
Springer-Verlag, pp. 76-79, 1996.
Guy, R. K. ``The Strong Law of Small Numbers.'' Amer. Math. Monthly 95, 697-712, 1988.
Noy, M. ``A Short Solution of a Problem in Combinatorial Geometry.'' Math. Mag. 69, 52-53, 1996.
Sloane, N. J. A. Sequences
A000124/M1041
and A000127/M1119
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Yaglom, A. M. and Yaglom, I. M. Problem 47. Challenging Mathematical Problems with Elementary Solutions, Vol. 1.
New York: Dover, 1987.
|
|
|
© 1996-9 Eric W. Weisstein