|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let two points be picked randomly from a unit ![]() -D Hypercube. The expected distance between the points
-D Hypercube. The expected distance between the points
![]() is then
is then
![\begin{displaymath}
{\textstyle{1\over 3}}n^{1/2}\leq \Delta(n)\leq ({\textstyle...
...1\over 3}\left[{1+2\left({1-{3\over 5n}}\right)^{1/2}}\right]}
\end{displaymath}](c4_85.gif) |
(1) |
Pick ![]() points
points ![]() , ...,
, ..., ![]() randomly in a unit
randomly in a unit ![]() -cube. Let
-cube. Let ![]() be the Convex Hull, so
be the Convex Hull, so
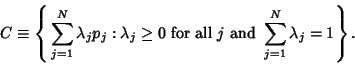 |
(2) |
| (3) |
| (4) |
| (5) |
| (6) |
Pick ![]() points on a Cube, and space them as far apart as possible. The best value known for the minimum straight
Line distance between any two points is given in the following table.
points on a Cube, and space them as far apart as possible. The best value known for the minimum straight
Line distance between any two points is given in the following table.
| 5 | 1.1180339887498 |
| 6 | 1.0606601482100 |
| 7 | 1 |
| 8 | 1 |
| 9 | 0.86602540378463 |
| 10 | 0.74999998333331 |
| 11 | 0.70961617562351 |
| 12 | 0.70710678118660 |
| 13 | 0.70710678118660 |
| 14 | 0.70710678118660 |
| 15 | 0.625 |
See also Cube Triangle Picking, Discrepancy Theorem, Point Picking
References
Anderssen, R. S.; Brent, R. P.; Daley, D. J.; and Moran, A. P. ``Concerning
Bolis, T. S. Solution to Problem E2629. ``Average Distance Between Two Points in a Box.'' Amer. Math. Monthly
85, 277-278, 1978.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/geom/geom.html
Ghosh, B. ``Random Distances within a Rectangle and Between Two Rectangles.'' Bull. Calcutta Math. Soc. 43, 17-24, 1951.
Holshouser, A. L.; King, L. R.; and Klein, B. G. Solution to Problem E3217, ``Minimum Average Distance Between Points in a Rectangle.''
Amer. Math. Monthly 96, 64-65, 1989.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 30, 1983.
Rényi, A. and Sulanke, R. ``Über die konvexe Hülle von
Rényi, A. and Sulanke, R. ``Über die konvexe Hülle von
Robbins, D. ``Average Distance Between Two Points in a Box.'' Amer. Math. Monthly 85, 278, 1978.
Santaló, L. A. Integral Geometry and Geometric Probability. Reading, MA: Addison-Wesley, 1976.
![]() and a Taylor Series Method.'' SIAM J. Appl. Math. 30, 22-30, 1976.
and a Taylor Series Method.'' SIAM J. Appl. Math. 30, 22-30, 1976.
![]() zufällig gewählten Punkten, I.''
Z. Wahrscheinlichkeits 2, 75-84, 1963.
zufällig gewählten Punkten, I.''
Z. Wahrscheinlichkeits 2, 75-84, 1963.
![]() zufällig gewählten Punkten, II.''
Z. Wahrscheinlichkeits 3, 138-147, 1964.
zufällig gewählten Punkten, II.''
Z. Wahrscheinlichkeits 3, 138-147, 1964.
|
|
|
© 1996-9 Eric W. Weisstein