|
|
|
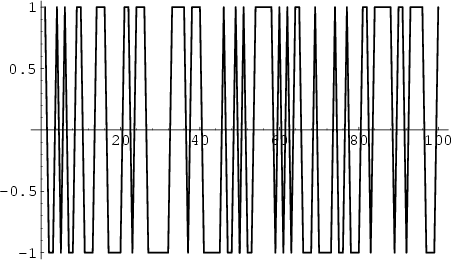
The function
| (1) |
 |
(2) |
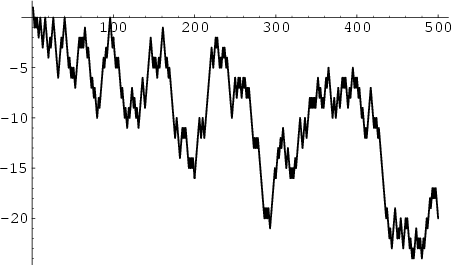
The Conjecture that the Summatory Function
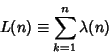 |
(3) |
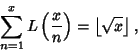 |
(4) |
|
|
|
|
|
(5) |
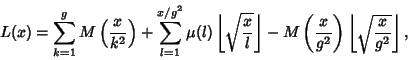 |
(6) |
See also Pólya Conjecture, Prime Factors, Riemann Zeta Function
References
Fawaz, A. Y. ``The Explicit Formula for
Lehman, R. S. ``On Liouville's Function.'' Math. Comput. 14, 311-320, 1960.
Sloane, N. J. A. Sequences
A028488 and
A002819/M0042
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Tanaka, M. ``A Numerical Investigation on Cumulative Sum of the Liouville Function.'' Tokyo J. Math. 3, 187-189, 1980.
![]() .'' Proc. London Math. Soc. 1, 86-103, 1951.
.'' Proc. London Math. Soc. 1, 86-103, 1951.
|
|
|
© 1996-9 Eric W. Weisstein