Simson Line

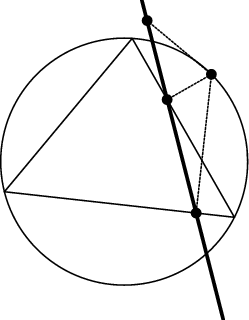
The Simson line is the Line containing the feet of the perpendiculars from a point on the Circumcircle of a Triangle to the sides (or their extensions) of the Triangle. The Simson line is sometimes known as the Wallace-Simson Line, since it does not appear in any work of Simson (Johnson 1929, p. 137).

The Angle between the Simson lines of two points $P$ and $P'$ is half the Angle of the arc $PP'$. The Simson line of any Vertex is the Altitude through that Vertex. The Simson line of a point opposite a Vertex is the corresponding side. If $T_1T_2T_3$ is the Simson line of a point $T$ of the Circumcircle, then the triangles $TT_1T_2$ and $TA_2A_1$ are directly similar.

See also Circumcircle

References

Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 40-41 and 43-45, 1967.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 137-139, 1929.