|
|
|
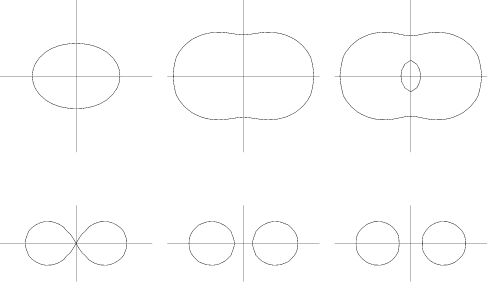
A curve with Cartesian equation
In the Formula of the curve given above, the Torus is formed from a Circle of Radius ![]() whose
center is rotated along a Circle of Radius
whose
center is rotated along a Circle of Radius ![]() . The value of
. The value of ![]() gives the distance of the cutting Plane
from the center of the Torus.
gives the distance of the cutting Plane
from the center of the Torus.
When ![]() , the curve consists of two Circles of Radius
, the curve consists of two Circles of Radius ![]() whose centers are at
whose centers are at ![]() and
and
![]() . If
. If ![]() , the curve consists of one point (the origin), while if
, the curve consists of one point (the origin), while if ![]() , no point lies on the curve. The
above curves have
, no point lies on the curve. The
above curves have
![]() , (3, 1, 2) (3, 0.8, 2), (3, 1, 4), (3, 1, 4.5), and (3, 0, 4.5).
, (3, 1, 2) (3, 0.8, 2), (3, 1, 4), (3, 1, 4.5), and (3, 0, 4.5).
References
MacTutor History of Mathematics Archive. ``Spiric Sections.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Spiric.html.