+ 
+ 
+ 
= 
+
+
+
=
AM是△ABC的BC边上的中线，则有AB2+AC2=2(AM2+BM2)
过点A作BC的垂线AM， 垂足为D．在Rt△ABD中，由勾股定理可知，AB2=AD2+BD2；同理，AC2=AD2+CD2，AM2=AD2+DM2
又BD=BM+DM，CD=CM−DM ，BM=CM，
故AB2+AC2=2AD2+BD2+CD2=2(AM2−DM2)+(BM+DM)2+(CM−DM)2 =2(AM2−DM2)+BM2+DM2+CM2+DM2
△ABC中，D是BC上任意一点，则有 AB2⋅CD+AC2⋅BD=AD2⋅BC+BD⋅CD⋅BC
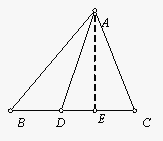
过A作BC的垂线，垂足为E，则有AB2=AE2+BE2 ，AC2=AE2+CE2，AD2=AE2+DE2，故AB2⋅CD+AC2⋅BD−AD2⋅BC=(AE2+BE2)⋅CD+(AE2+CE2)⋅BD−(AE2+DE2)⋅BC=AE2(CD+BD−BC)+BE2⋅CD+CE2⋅BD−DE2⋅BC =BE2⋅CD+CE2⋅BD−DE2⋅BC=(BD+DE)2⋅CD+(CD−DE)2⋅BD =BE2⋅CD+CE2⋅BD−DE2⋅BC=(BD+DE)2⋅CD+(CD−DE)2⋅BD −DE2⋅BC=(BD2+DE2+2BD⋅DE)⋅CD+(CD2+DE2−2CD⋅DE)⋅BD −DE2⋅BC=BD2⋅CD+CD2⋅BD+DE2⋅BC−DE2⋅BC=BD2⋅CD+CD2⋅BD
即AB2⋅CD+AC2⋅BD=AD2⋅BC+BD⋅CD⋅BC
由斯德瓦尔特定理可以得出很多有用的结论，比如上例，令本例中BD=CD，则很快得出上例的结论以及中线长的公式，一般地，只要ΔABC的三条边已知，BC上一点D的位置已知，则AD的长度便可直接求出来．此外，用余弦定理证明斯德瓦尔特定理也是很快的：
在△ABC中，由余弦定理可知，AB2=AD2+BD2−2AD⋅BDcos∠ADB ；
在△ACD中，由余弦定理可知，AC2=AD2+CD2−2AD⋅CDcos∠ADC ;
故AB2⋅CD+AC2⋅BD−AD2⋅BC=AD2⋅CD+BD2⋅CD+AD2⋅BD+CD2⋅BD −AD2⋅BC=AD2⋅BC+BD⋅CD⋅BC−AD2⋅BC=BD⋅CD⋅BC