Constructible Polygon

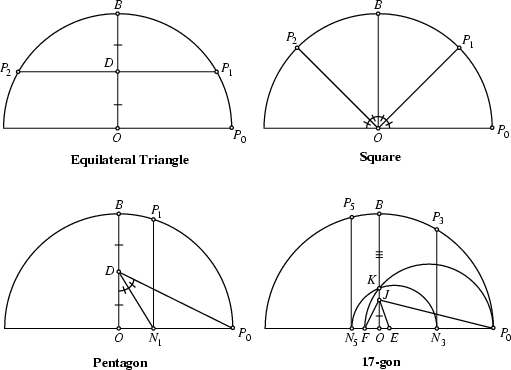
$\begin{figure}\begin{center}\BoxedEPSF{PolygonConstruction.epsf scaled 700}\end{center}\end{figure}$

Compass and Straightedge constructions dating back to Euclid were capable of inscribing regular polygons of 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 40, 48, 64, ..., sides. However, this listing is not a complete enumeration of ``constructible'' polygons. A regular -gon ( $n\geq 3$ ) can be constructed by Straightedge and Compass Iff

$\begin{displaymath} n=2^k p_1p_2\cdots p_s, \end{displaymath}$

where

is in Integer $\geq 0$ and the

are distinct Fermat Primes. Fermat Numbers are of the form

$\begin{displaymath} F_m=2^{2^m}+1, \end{displaymath}$

where

is an Integer $\geq 0$ . The only known Primes of this form are 3, 5, 17, 257, and 65537. The fact that this condition was Sufficient was first proved by Gauß

in 1796 when he was 19 years old. That this condition was also Necessary was not explicitly proven by Gauß,

and the first proof of this fact is credited to Wantzel (1836).

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 94-96, 1987.

Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 119, 1996.

De Temple, D. W. ``Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions.'' Amer. Math. Monthly 98, 97-108, 1991.

Dixon, R. ``Compass Drawings.'' Ch. 1 in Mathographics. New York: Dover, pp. 1-78, 1991.

Gauss, C. F. §365 and 366 in Disquisitiones Arithmeticae. Leipzig, Germany, 1801. Translated by A. A. Clarke. New Haven, CT: Yale University Press, 1965.

Kazarinoff, N. D. ``On Who First Proved the Impossibility of Constructing Certain Regular Polygons with Ruler and Compass Alone.'' Amer. Math. Monthly 75, 647-648, 1968.

Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 137-138, 1990.

Wantzel, M. L. ``Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas.'' J. Math. pures appliq. 1, 366-372, 1836.