|
|
|
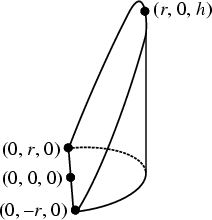
The solid cut from a Cylinder by a tilted Plane passing through a Diameter of the base. It is also
called a Cylindrical Hoof. Let the height of the wedge be ![]() and the radius of the Cylinder from
which it is cut
and the radius of the Cylinder from
which it is cut ![]() . Then plugging the points
. Then plugging the points ![]() ,
, ![]() , and
, and ![]() into
the 3-point equation for a
Plane gives the equation for the plane as
into
the 3-point equation for a
Plane gives the equation for the plane as
| (1) |
| (2) | |||
| (3) | |||
| (4) |
| (5) |
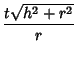 |
(6) | ||
| (7) |
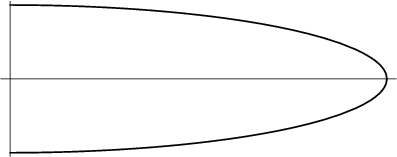
The length of the tongue (measured down its middle) is obtained by plugging ![]() into the above equation
for
into the above equation
for ![]() , which becomes
, which becomes
| (8) |
| (9) |
See also Conical Wedge, Cylindrical Segment
|
|
|
© 1996-9 Eric W. Weisstein