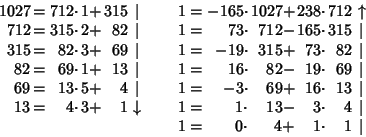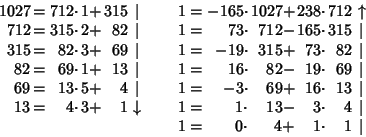A linear Diophantine equation (in two variables) is an equation of the general form
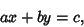 |
(1) |
where solutions are sought with 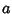 ,
,  , and
, and 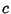 Integers. Such equations can be solved completely, and
the first known solution was constructed by Brahmagupta. Consider the equation
Integers. Such equations can be solved completely, and
the first known solution was constructed by Brahmagupta. Consider the equation
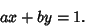 |
(2) |
Now use a variation of the Euclidean Algorithm, letting 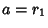 and
and 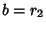
Starting from the bottom gives
so
Continue this procedure all the way back to the top.
Take as an example the equation
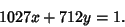 |
(10) |
Proceed as follows.
The solution is therefore  ,
, 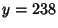 . The above procedure can be simplified by noting that the two left-most
columns are offset by one entry and alternate signs, as they must since
. The above procedure can be simplified by noting that the two left-most
columns are offset by one entry and alternate signs, as they must since
so the Coefficients of 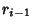 and
and 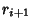 are the same and
are the same and
 |
(14) |
Repeating the above example using this information therefore gives
and we recover the above solution.
Call the solutions to
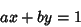 |
(15) |
 and
and 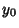 . If the signs in front of
. If the signs in front of 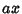 or
or 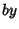 are Negative, then solve the above equation and take the signs of
the solutions from the following table:
are Negative, then solve the above equation and take the signs of
the solutions from the following table:
In fact, the solution to the equation
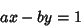 |
(16) |
is equivalent to finding the Continued Fraction for 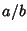 , with
, with 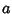 and
and  Relatively Prime (Olds 1963).
If there are
Relatively Prime (Olds 1963).
If there are  terms in the fraction, take the
terms in the fraction, take the 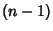 th convergent
th convergent
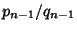 . But
. But
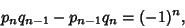 |
(17) |
so one solution is
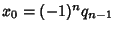 ,
,
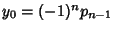 , with a general solution
, with a general solution
with  an arbitrary Integer. The solution in terms of smallest Positive Integers is given
by choosing an appropriate
an arbitrary Integer. The solution in terms of smallest Positive Integers is given
by choosing an appropriate  .
.
Now consider the general first-order equation of the form
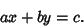 |
(20) |
The Greatest Common Divisor
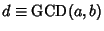 can be divided through yielding
can be divided through yielding
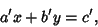 |
(21) |
where 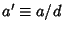 ,
, 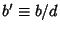 , and
, and  . If
. If 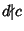 , then
, then  is not an Integer and the
equation cannot have a solution in Integers. A necessary and sufficient condition for the general
first-order equation to have solutions in Integers is therefore that
is not an Integer and the
equation cannot have a solution in Integers. A necessary and sufficient condition for the general
first-order equation to have solutions in Integers is therefore that 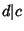 . If this is the case, then
solve
. If this is the case, then
solve
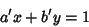 |
(22) |
and multiply the solutions by  , since
, since
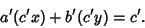 |
(23) |
References
Courant, R. and Robbins, H. ``Continued Fractions. Diophantine Equations.'' §2.4 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 49-51, 1996.
Dickson, L. E. ``Linear Diophantine Equations and Congruences.'' Ch. 2 in
History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, pp. 41-99, 1952.
Olds, C. D. Ch. 2 in Continued Fractions. New York: Random House, 1963.
© 1996-9 Eric W. Weisstein
1999-05-24