A family of Functors 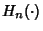 from the Category of pairs of Topological
Spaces and continuous maps, to the Category of Abelian Groups and group
homomorphisms satisfies the Eilenberg-Steenrod axioms if the following conditions hold.
from the Category of pairs of Topological
Spaces and continuous maps, to the Category of Abelian Groups and group
homomorphisms satisfies the Eilenberg-Steenrod axioms if the following conditions hold.
- 1. Long Exact Sequence of a Pair Axiom. For every pair
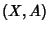 , there is a natural long exact sequence
, there is a natural long exact sequence
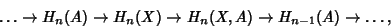 |
(1) |
where the Map
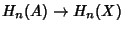 is induced by the Inclusion Map
is induced by the Inclusion Map  and
and
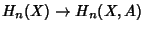 is induced by
the Inclusion Map
is induced by
the Inclusion Map
 . The Map
. The Map
 is called the Boundary Map.
is called the Boundary Map.
- 2. Homotopy Axiom. If
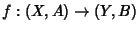 is homotopic to
is homotopic to
 , then their Induced
Maps
, then their Induced
Maps
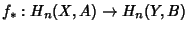 and
and
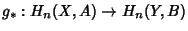 are the same.
are the same.
- 3. Excision Axiom. If
 is a Space with Subspaces
is a Space with Subspaces 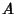 and
and 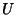 such that the
Closure of
such that the
Closure of 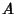 is contained in the interior of
is contained in the interior of 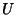 , then the Inclusion Map
, then the Inclusion Map
 induces
an isomorphism
induces
an isomorphism
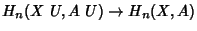 .
.
- 4. Dimension Axiom. Let
 be a single point space.
be a single point space. 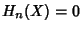 unless
unless 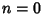 , in which case
, in which case 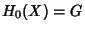 where
where 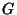 are some Groups. The
are some Groups. The 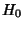 are called the Coefficients of the Homology theory
are called the Coefficients of the Homology theory 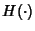 .
.
These are the axioms for a generalized homology theory. For a cohomology theory, instead of requiring that 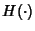 be a
Functor, it is required to be a co-functor (meaning the Induced Map points in the opposite direction). With
that modification, the axioms are essentially the same (except that all the induced maps point backwards).
be a
Functor, it is required to be a co-functor (meaning the Induced Map points in the opposite direction). With
that modification, the axioms are essentially the same (except that all the induced maps point backwards).
See also Aleksandrov-Cech Cohomology
© 1996-9 Eric W. Weisstein
1999-05-25
![]() from the Category of pairs of Topological
Spaces and continuous maps, to the Category of Abelian Groups and group
homomorphisms satisfies the Eilenberg-Steenrod axioms if the following conditions hold.
from the Category of pairs of Topological
Spaces and continuous maps, to the Category of Abelian Groups and group
homomorphisms satisfies the Eilenberg-Steenrod axioms if the following conditions hold.
![]() be a
Functor, it is required to be a co-functor (meaning the Induced Map points in the opposite direction). With
that modification, the axioms are essentially the same (except that all the induced maps point backwards).
be a
Functor, it is required to be a co-functor (meaning the Induced Map points in the opposite direction). With
that modification, the axioms are essentially the same (except that all the induced maps point backwards).