|
|
|

In 1-D, the Gaussian function is the function from the Gaussian Distribution,
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
In 2-D, the circular Gaussian function is the distribution function for uncorrelated variables ![]() and
and ![]() having a
Gaussian Bivariate Distribution and equal Standard Deviation
having a
Gaussian Bivariate Distribution and equal Standard Deviation
![]() ,
,
| (9) |
| (10) |
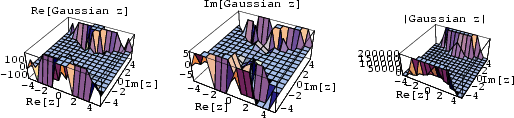
The above plots show the real and imaginary parts of
![]() together with the complex absolute value
together with the complex absolute value
![]() .
.

The Gaussian function can also be used as an Apodization Function, shown above with the corresponding Instrument Function.
The Hypergeometric Function is also sometimes known as the Gaussian function.
See also Erf, Erfc, Fourier Transform--Gaussian, Gaussian Bivariate Distribution, Gaussian Distribution, Normal Distribution
References
MacTutor History of Mathematics Archive. ``Frequency Curve.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Frequency.html.
|
|
|
© 1996-9 Eric W. Weisstein