|
|
|
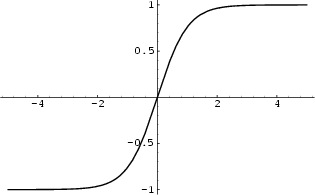
By way of analogy with the usual Tangent
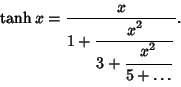
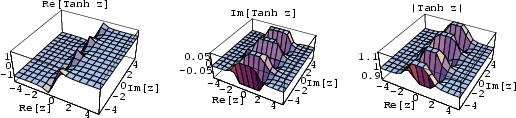
See also Bernoulli Number, Catenary, Correlation Coefficient--Gaussian Bivariate Distribution, Fibonacci Hyperbolic Tangent, Fisher's z'-Transformation, Hyperbolic Cotangent, Lorentz Group, Mercator Projection, Oblate Spheroidal Coordinates, Pseudosphere, Surface of Revolution, Tangent, Tractrix, Tractroid
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Hyperbolic Functions.'' §4.5 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 83-86, 1972.
Spanier, J. and Oldham, K. B. ``The Hyperbolic Tangent
![]() and Cotangent
and Cotangent ![]() Functions.''
Ch. 30 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 279-284, 1987.
Functions.''
Ch. 30 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 279-284, 1987.