|
|
|
The pedal Circle of a point ![]() in a Triangle is the Circle through the feet of the perpendiculars
from
in a Triangle is the Circle through the feet of the perpendiculars
from ![]() to the sides of the Triangle (the Circumcircle about the Pedal Triangle). When
to the sides of the Triangle (the Circumcircle about the Pedal Triangle). When ![]() is on a
side of the Triangle, the line between the two perpendiculars is called the Pedal Line. Given four points,
no three of which are Collinear, then the four Pedal Circles of each point for the
Triangle formed by the other three have a common point through which the Nine-Point Circles of the four Triangles pass. The radius of the pedal circle of a point
is on a
side of the Triangle, the line between the two perpendiculars is called the Pedal Line. Given four points,
no three of which are Collinear, then the four Pedal Circles of each point for the
Triangle formed by the other three have a common point through which the Nine-Point Circles of the four Triangles pass. The radius of the pedal circle of a point ![]() is
is
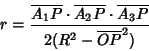
See also Miquel Point, Nine-Point Circle, Pedal Triangle
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, 1929.