|
|
|
Perfect numbers are Integers ![]() such that
such that
| (1) |
| (2) |
Perfect numbers are intimately connected with a class of numbers known as Mersenne Primes.
This can be demonstrated by considering a perfect number ![]() of the form
of the form ![]() where
where ![]() is Prime. Then
is Prime. Then
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| # | ||
| 1 | 2 | 6 |
| 2 | 3 | 28 |
| 3 | 5 | 496 |
| 4 | 7 | 8128 |
| 5 | 13 | 33550336 |
| 6 | 17 | 8589869056 |
| 7 | 19 | 137438691328 |
| 8 | 31 | 2305843008139952128 |
All Even perfect numbers are of this form, as was proved by Euler ![]() in a posthumous paper. The only even perfect number
of the form
in a posthumous paper. The only even perfect number
of the form ![]() is 28 (Makowski 1962).
is 28 (Makowski 1962).
It is not known if any Odd perfect numbers exist, although numbers up to ![]() have been checked (Brent et al. 1991,
Guy 1994) without success, improving the result of Tuckerman (1973), who checked odd numbers up to
have been checked (Brent et al. 1991,
Guy 1994) without success, improving the result of Tuckerman (1973), who checked odd numbers up to ![]() . Euler
. Euler ![]() showed that an Odd perfect number, if it exists, must be of the form
showed that an Odd perfect number, if it exists, must be of the form
| (10) |
Every perfect number of the form
![]() can be written
can be written
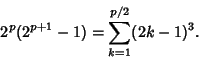 |
(11) |
| (12) | |||
| (13) | |||
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
If ![]() ,
, ![]() is said to be an Abundant Number. If
is said to be an Abundant Number. If ![]() ,
, ![]() is said to be a Deficient Number.
And if
is said to be a Deficient Number.
And if ![]() for a Positive Integer
for a Positive Integer ![]() ,
, ![]() is said to be a Multiperfect Number of order
is said to be a Multiperfect Number of order
![]() .
.
See also Abundant Number, Aliquot Sequence, Amicable Numbers, Deficient Number, Divisor Function, e-Perfect Number, Harmonic Number, Hyperperfect Number, Infinary Perfect Number, Mersenne Number, Mersenne Prime, Multiperfect Number, Multiplicative Perfect Number, Pluperfect Number, Pseudoperfect Number, Quasiperfect Number, Semiperfect Number, Smith Number, Sociable Numbers, Sublime Number, Superperfect Number, Unitary Perfect Number, Weird Number
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 66-67, 1987.
Brent, R. P.; Cohen, G. L. L.; and te Riele, H. J. J. ``Improved Techniques for Lower Bounds for Odd Perfect Numbers.''
Math. Comput. 57, 857-868, 1991.
Conway, J. H. and Guy, R. K. ``Perfect Numbers.'' In The Book of Numbers. New York: Springer-Verlag, pp. 136-137, 1996.
Dickson, L. E. ``Notes on the Theory of Numbers.'' Amer. Math. Monthly 18, 109-111, 1911.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea,
pp. 3-33, 1952.
Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, p. 75, 1990.
Eaton, C. F. ``Problem 1482.'' Math. Mag. 68, 307, 1995.
Eaton, C. F. ``Perfect Number in Terms of Triangular Numbers.'' Solution to Problem 1482. Math. Mag. 69, 308-309, 1996.
Gardner, M. ``Perfect, Amicable, Sociable.'' Ch. 12 in
Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage,
pp. 160-171, 1978.
Guy, R. K. ``Perfect Numbers.'' §B1 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 145, 1994.
Kraitchik, M. ``Mersenne Numbers and Perfect Numbers.'' §3.5 in Mathematical Recreations. New York: W. W. Norton,
pp. 70-73, 1942.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 145 and 147-151, 1979.
Makowski, A. ``Remark on Perfect Numbers.'' Elemente Math. 17, 109, 1962.
Powers, R. E. ``The Tenth Perfect Number.'' Amer. Math. Monthly 18, 195-196, 1911.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 1-13 and 25-29, 1993.
Singh, S. Fermat's Enigma: The Epic Quest to Solve the World's Greatest Mathematical Problem.
New York: Walker, pp. 11-13, 1997.
Sloane, N. J. A. Sequence
A000396/M4186
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Tuckerman, B. ``Odd Perfect Numbers: A Search Procedure, and a New Lower Bound of
Tuckerman, B. ``A Search Procedure and Lower Bound for Odd Perfect Numbers.'' Math. Comp. 27, 943-949, 1973.
Zachariou, A. and Zachariou, E. ``Perfect, Semi-Perfect and Ore Numbers.'' Bull. Soc. Math. Grèce (New Ser.) 13, 12-22, 1972.
![]() .'' Not. Amer. Math. Soc. 15, 226, 1968.
.'' Not. Amer. Math. Soc. 15, 226, 1968.
|
|
|
© 1996-9 Eric W. Weisstein