|
|
|
A sequence of numbers generated by a Recurrence Relation is called a recurrence sequence. Perhaps the most famous recurrence sequence is the Fibonacci Numbers.
If a sequence ![]() with
with ![]() is described by a two-term linear recurrence relation of the form
is described by a two-term linear recurrence relation of the form
| (1) |
| (2) |
| (3) |
| (4) | |||
| (5) |
The general second-order linear recurrence
| (6) |

![$x_n=\sum_{k=0}^{n-2}{\left\lfloor{{\textstyle{1\over 2}}(n+k-2)}\right\rfloor \...
...)/2}\right\rfloor } {x_1}^{[n+k{\rm\ (mod\ }2)]}{x_2}^{[n+k+1{\rm\ (mod\ }2)]}.$](r_960.gif)
|
(7) |
|
|
|
|
|
(8) |
The general linear third-order recurrence
| (9) |
|
|
|
|
|
|
|
|
(10) |
| (11) |
A Quotient-Difference Table eventually yields a line of 0s Iff the starting sequence is defined by a linear recurrence relation.
A linear second-order recurrence
| (12) |
| (13) |
| (14) |
| (15) |
| (16) | |||
| (17) | |||
| (18) | |||
| (19) |
| (20) | |||
| (21) | |||
| (22) | |||
| (23) |
Let
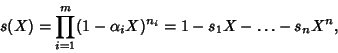 |
(24) |
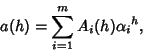 |
(25) |
| (26) |
The terms in a general recurrence sequence belong to a finitely generated Ring over the Integers, so
it is impossible for every Rational Number to occur in any finitely generated recurrence sequence. If a recurrence
sequence vanishes infinitely often, then it vanishes on an arithmetic progression with a common difference 1 that depends only
on the roots. The number of values that a recurrence sequence can take on infinitely often is bounded by some Integer
![]() that depends only on the roots. There is no recurrence sequence in which each Integer occurs infinitely often, or
in which every Gaussian Integer occurs (Myerson and van der Poorten 1995).
that depends only on the roots. There is no recurrence sequence in which each Integer occurs infinitely often, or
in which every Gaussian Integer occurs (Myerson and van der Poorten 1995).
Let ![]() be a bound so that a nondegenerate Integer recurrence sequence of order
be a bound so that a nondegenerate Integer recurrence sequence of order ![]() takes the value zero at least
takes the value zero at least
![]() times. Then
times. Then ![]() ,
, ![]() , and
, and ![]() (Myerson and van der Poorten 1995). The maximal case for
(Myerson and van der Poorten 1995). The maximal case for
![]() is
is
| (27) |
| (28) |
| (29) |
| (30) |
See also Binet Forms, Binet's Formula, Fast Fibonacci Transform, Fibonacci Sequence, Lucas Sequence, Quotient-Difference Table, Skolem-Mahler-Lerch Theorem
References
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Beukers, F. ``The Zero-Multiplicity of Ternary Recurrences.'' Composito Math. 77, 165-177, 1991.
Myerson, G. and van der Poorten, A. J. ``Some Problems Concerning Recurrence Sequences.'' Amer. Math. Monthly 102, 698-705, 1995.
|
|
|
© 1996-9 Eric W. Weisstein