|
|
|
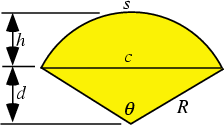
A Wedge obtained by taking a portion of a Circle with Central Angle ![]() radians (180°),
illustrated above as the shaded region. A sector of
radians (180°),
illustrated above as the shaded region. A sector of ![]() radians would be a Semicircle. Let
radians would be a Semicircle. Let ![]() be the radius of
the Circle,
be the radius of
the Circle, ![]() the Chord length,
the Chord length, ![]() the Arc Length,
the Arc Length, ![]() the height of the arced portion, and
the height of the arced portion, and ![]() the
height of the triangular portion. Then
the
height of the triangular portion. Then
| (1) | |||
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) |
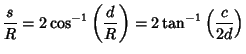 |
|||
| (10) |
| (11) |
See also Circle-Circle Intersection, Lens, Obtuse Triangle, Segment
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 125, 1987.
|
|
|
© 1996-9 Eric W. Weisstein