Trigonometric functions of 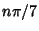 for
for  an integer cannot be expressed in terms of sums, products, and finite root
extractions on real rational numbers because 7 is not a Fermat Prime. This also means that the Heptagon
is not a Constructible Polygon.
an integer cannot be expressed in terms of sums, products, and finite root
extractions on real rational numbers because 7 is not a Fermat Prime. This also means that the Heptagon
is not a Constructible Polygon.
However, exact expressions involving roots of complex numbers can still be derived using the trigonometric identity
![\begin{displaymath}
\sin(n\alpha)=2\sin[(n-1)\alpha]\cos\alpha-\sin[(n-2)\alpha].
\end{displaymath}](t_1921.gif) |
(1) |
The case  gives
Rewrite this using the identity
gives
Rewrite this using the identity
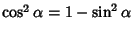 ,
,

|
|

|
(3) |
Now, let
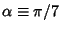 and
and
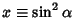 , then
, then
 |
(4) |
which is a Cubic Equation in 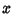 . The Roots are numerically found to be
. The Roots are numerically found to be
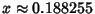 ,
,
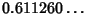 ,
,
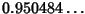 . But
. But
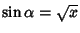 , so these Roots correspond to
, so these Roots correspond to
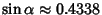 ,
,
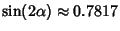 ,
,
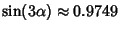 . By Newton's
Relation
. By Newton's
Relation
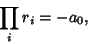 |
(5) |
we have
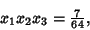 |
(6) |
or
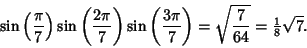 |
(7) |
Similarly,
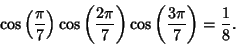 |
(8) |
The constants of the Cubic Equation are given by
The Discriminant is then
so there are three distinct Real Roots. Finding the first one,
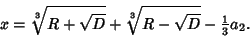 |
(12) |
Writing
 |
(13) |
plugging in from above, and anticipating that the solution we have picked corresponds to 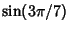 ,
,
See also Heptagon
© 1996-9 Eric W. Weisstein
1999-05-26
![]() for
for ![]() an integer cannot be expressed in terms of sums, products, and finite root
extractions on real rational numbers because 7 is not a Fermat Prime. This also means that the Heptagon
is not a Constructible Polygon.
an integer cannot be expressed in terms of sums, products, and finite root
extractions on real rational numbers because 7 is not a Fermat Prime. This also means that the Heptagon
is not a Constructible Polygon.
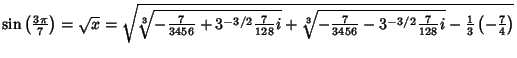
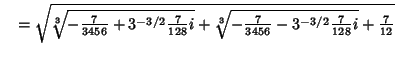
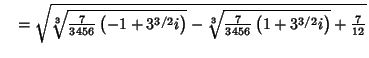
![$\quad = \sqrt{{1\over 12}\left[{{\root 3 \of{{7\over 2}\left({-1+3^{3/2} i}\right)}}- {\root 3\of{{7\over 2}\left({1+3^{3/2} i}\right)}}+7}\right]}.$](t_1959.gif)