|
|
|
First studied by Huygens ![]() when he was considering clocks without pendula
when he was considering clocks without pendula ![]() for use on
ships at sea. He used the circle involute in his first pendulum clock in an attempt to force the pendulum to swing in the
path of a Cycloid.
for use on
ships at sea. He used the circle involute in his first pendulum clock in an attempt to force the pendulum to swing in the
path of a Cycloid.
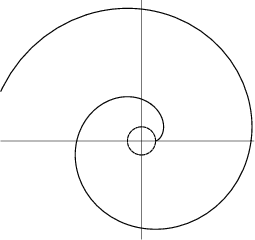
For a Circle with ![]() , the parametric equations of the circle
and their derivatives are given by
, the parametric equations of the circle
and their derivatives are given by
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) | |||
| (7) |

The Arc Length, Curvature, and Tangential Angle are
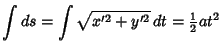 |
(8) | ||
| (9) | |||
| (10) |
| (11) |
See also Circle, Circle Evolute, Ellipse Involute, Involute
References
Gray, A. Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, p. 83, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 190-191, 1972.
MacTutor History of Mathematics Archive. ``Involute of a Circle.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Involute.html.
|
|
|
© 1996-9 Eric W. Weisstein