|
|
|
The ![]() -function is defined as
-function is defined as
| (1) |
| (2) |
| (3) |
![$\displaystyle {[f^{24}(z)-16]^3\over f^{24}(z)}$](j_16.gif) |
(4) | ||
![$\displaystyle {[{f_1}^{24}(z)+16]^3\over {f_1}^{24}(z)}$](j_17.gif) |
(5) | ||
![$\displaystyle {[{f_2}^{24}(z)+16]^3\over {f_2}^{24}(z)}$](j_18.gif) |
(6) | ||
| (7) | |||
| (8) |
The ![]() -function is a Meromorphic function on the upper half of the Complex Plane which is invariant with
respect to the Special Linear Group
-function is a Meromorphic function on the upper half of the Complex Plane which is invariant with
respect to the Special Linear Group ![]() . It has a Fourier Series
. It has a Fourier Series
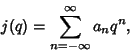 |
(9) |
| (10) |
Then all of the Coefficients in the Laurent Series
|
|
|
|
|
|
|
|
(11) |
| (12) |
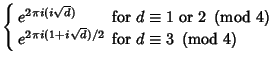 |
|||
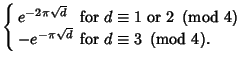 |
(13) |
The numbers whose Laurent Series give Integers are those with Class Number 1. But these
are precisely the Heegner Numbers ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . The
greater (in Absolute Value) the Heegner Number
. The
greater (in Absolute Value) the Heegner Number ![]() , the closer to an Integer is the expression
, the closer to an Integer is the expression
![]() , since the initial term in
, since the initial term in ![]() is the largest and subsequent terms are the smallest. The best
approximations with
is the largest and subsequent terms are the smallest. The best
approximations with ![]() are therefore
are therefore
| (14) | |||
| (15) | |||
| (16) |
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) | |||
| (23) | |||
| (24) | |||
| (25) |
![]() ,
,
![]() , and
, and
![]() are also Almost Integers. These
correspond to binary quadratic forms with discriminants
are also Almost Integers. These
correspond to binary quadratic forms with discriminants ![]() ,
, ![]() , and
, and ![]() , all of which have Class Number two
and were noted by Ramanujan
, all of which have Class Number two
and were noted by Ramanujan ![]() (Berndt 1994).
(Berndt 1994).
It turns out that the ![]() -function also is important in the Classification Theorem for finite simple groups, and
that the factors of the orders of the Sporadic Groups, including the celebrated Monster
Group, are also related.
-function also is important in the Classification Theorem for finite simple groups, and
that the factors of the orders of the Sporadic Groups, including the celebrated Monster
Group, are also related.
See also Almost Integer, Klein's Absolute Invariant, Weber Functions
References
Atkin, A. O. L. and Morain, F. ``Elliptic Curves and Primality Proving.'' Math. Comput. 61, 29-68, 1993.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 90-91, 1994.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 117-118, 1987.
Cohn, H. Introduction to the Construction of Class Fields. New York: Dover, p. 73, 1994.
Conway, J. H. and Guy, R. K. ``The Nine Magic Discriminants.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 224-226, 1996.
Morain, F. ``Implementation of the Atkin-Goldwasser-Kilian Primality Testing Algorithm.'' Rapport de Récherche 911, INRIA, Oct. 1988.
Rankin, R. A. Modular Forms. New York: Wiley, 1985.
Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, p. 199, 1977.
Serre, J. P. Cours d'arithmétique. Paris: Presses Universitaires de France, 1970.
Silverman, J. H. The Arithmetic of Elliptic Curves. New York: Springer-Verlag, p. 339, 1986.
Sloane, N. J. A. Sequence
A000521/M5477
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, 1979.
![]() Weisstein, E. W. ``
Weisstein, E. W. ``![]() -Function.'' Mathematica notebook jFunction.m.
-Function.'' Mathematica notebook jFunction.m.
|
|
|
© 1996-9 Eric W. Weisstein