- 1. If the sides of the Pedal Triangle of a point
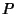 meet the corresponding sides of a Triangle
meet the corresponding sides of a Triangle
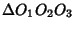 at
at 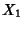 ,
, 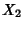 , and
, and 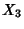 , respectively, then
, respectively, then  ,
, 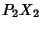 ,
, 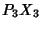 meet at a point
meet at a point 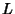 common to the Circles
common to the Circles 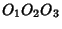 and
and 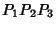 . In other words,
. In other words, 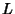 is one of the intersections
of the Nine-Point Circle of
is one of the intersections
of the Nine-Point Circle of 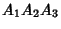 and the Pedal Circle of
and the Pedal Circle of 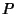 .
.
- 2. If a point moves on a fixed line through the Circumcenter, then its Pedal Circle passes
through a fixed point on the Nine-Point Circle.
- 3. The Pedal Circle of a point is tangent to the Nine-Point Circle Iff the point and its
Isogonal Conjugate lie on a Line through the Orthocenter.
Feuerbach's Theorem is a special case of this theorem.
See also Circumcenter, Feuerbach's Theorem, Isogonal Conjugate, Nine-Point Circle, Orthocenter,
Pedal Circle
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 245-247, 1929.
© 1996-9 Eric W. Weisstein
1999-05-26