Define a Spherical Triangle on the surface of a unit Sphere, centered at a point 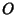 , with vertices
, with vertices 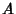 ,
, 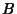 ,
and
,
and 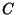 . Define Angles
. Define Angles
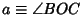 ,
,
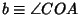 , and
, and
 . Let the
Angle between Planes
. Let the
Angle between Planes 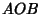 and
and 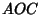 be
be 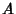 , the Angle between Planes
, the Angle between Planes
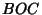 and
and 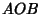 be
be 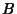 , and the Angle between Planes
, and the Angle between Planes 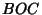 and
and 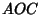 be
be 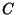 . Define the
Vectors
. Define the
Vectors
Then
Equivalently,
Since these two expressions are equal, we obtain the identity
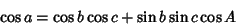 |
(6) |
The identity
where
![$[{\bf a}, {\bf b}, {\bf c}]$](s2_1273.gif) is the Scalar Triple Product, gives a spherical analog of the Law of Sines,
is the Scalar Triple Product, gives a spherical analog of the Law of Sines,
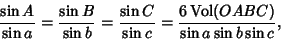 |
(8) |
where
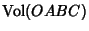 is the Volume of the Tetrahedron. From (7) and (8), it follows that
is the Volume of the Tetrahedron. From (7) and (8), it follows that
These are the fundamental equalities of spherical trigonometry.
There are also spherical analogs of the Law of Cosines for the sides of a spherical triangle,
and the angles of a spherical triangle,
(Beyer 1987), as well as the Law of Tangents
![\begin{displaymath}
{\tan[{\textstyle{1\over 2}}(a-b)]\over\tan[{\textstyle{1\ov...
...style{1\over 2}}(A-B)]\over\tan[{\textstyle{1\over 2}}(A+B)]}.
\end{displaymath}](s2_1292.gif) |
(17) |
Let
then the half-angle formulas are
where
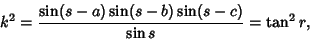 |
(23) |
and the half-side formulas are
where
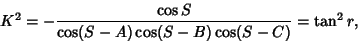 |
(27) |
where  is the Radius of the Sphere on which the spherical triangle lies.
is the Radius of the Sphere on which the spherical triangle lies.
Additional formulas include the Haversine formulas
Gauss's Formulas
and Napier's Analogies
(Beyer 1987).
See also Angular Defect, Descartes Total Angular Defect, Gauss's Formulas, Girard's Spherical Excess
Formula, Law of Cosines, Law of Sines, Law of Tangents, L'Huilier's Theorem, Napier's
Analogies, Spherical Excess, Spherical Geometry, Spherical Polygon, Spherical Triangle
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 131 and 147-150, 1987.
Danby, J. M. Fundamentals of Celestial Mechanics, 2nd ed., rev. ed. Richmond, VA: Willmann-Bell, 1988.
Smart, W. M. Text-Book on Spherical Astronomy, 6th ed. Cambridge, England: Cambridge University Press, 1960.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , with vertices
, with vertices ![]() ,
, ![]() ,
and
,
and ![]() . Define Angles
. Define Angles
![]() ,
,
![]() , and
, and
![]() . Let the
Angle between Planes
. Let the
Angle between Planes ![]() and
and ![]() be
be ![]() , the Angle between Planes
, the Angle between Planes
![]() and
and ![]() be
be ![]() , and the Angle between Planes
, and the Angle between Planes ![]() and
and ![]() be
be ![]() . Define the
Vectors
. Define the
Vectors
![$\displaystyle {\vert(\hat {\bf a}\times \hat {\bf b})\times (\hat {\bf a}\times...
...}]+\hat {\bf b}[\hat {\bf a},\hat {\bf a},\hat {\bf c}]\vert\over \sin b\sin c}$](s2_1271.gif)
![$\displaystyle {[\hat {\bf a},\hat {\bf b},\hat {\bf c}]\over \sin b\sin c},$](s2_1272.gif)
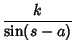
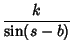
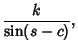
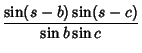
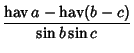
![$\displaystyle {\sin[{\textstyle{1\over 2}}(a-b)]\over\sin({\textstyle{1\over 2}}c)}$](s2_1316.gif)
![$\displaystyle {\sin[{\textstyle{1\over 2}}(A-B)]\over\cos({\textstyle{1\over 2}}C)}$](s2_1317.gif)
![$\displaystyle {\sin[{\textstyle{1\over 2}}(a+b)]\over\sin({\textstyle{1\over 2}}c)}$](s2_1318.gif)
![$\displaystyle {\cos[{\textstyle{1\over 2}}(A-B)]\over\sin({\textstyle{1\over 2}}C)}$](s2_1319.gif)
![$\displaystyle {\cos[{\textstyle{1\over 2}}(a-b)]\over\cos({\textstyle{1\over 2}}c)}$](s2_1320.gif)
![$\displaystyle {\sin[{\textstyle{1\over 2}}(A+B)]\over\cos({\textstyle{1\over 2}}C)}$](s2_1321.gif)
![$\displaystyle {\cos[{\textstyle{1\over 2}}(a+b)]\over\cos({\textstyle{1\over 2}}c)}$](s2_1322.gif)
![$\displaystyle {\cos[{\textstyle{1\over 2}}(A+B)]\over\sin({\textstyle{1\over 2}}C)},$](s2_1323.gif)
![$\displaystyle {\sin[{\textstyle{1\over 2}}(A-B)]\over\sin[{\textstyle{1\over 2}}(A+B)]}$](s2_1324.gif)
![$\displaystyle {\tan[{\textstyle{1\over 2}}(a-b)]\over\tan({\textstyle{1\over 2}}c)}$](s2_1325.gif)
![$\displaystyle {\cos[{\textstyle{1\over 2}}(A-B)]\over\cos[{\textstyle{1\over 2}}(A+B)]}$](s2_1326.gif)
![$\displaystyle {\tan[{\textstyle{1\over 2}}(a+b)]\over\tan({\textstyle{1\over 2}}c)}$](s2_1327.gif)
![$\displaystyle {\sin[{\textstyle{1\over 2}}(a-b)]\over\sin[{\textstyle{1\over 2}}(a+b)]}$](s2_1328.gif)
![$\displaystyle {\tan[{\textstyle{1\over 2}}(A-B)]\over\cot({\textstyle{1\over 2}}C)}$](s2_1329.gif)
![$\displaystyle {\cos[{\textstyle{1\over 2}}(a-b)]\over\cos[{\textstyle{1\over 2}}(a+b)]}$](s2_1330.gif)
![$\displaystyle {\tan[{\textstyle{1\over 2}}(A+B)]\over\cot({\textstyle{1\over 2}}C)}$](s2_1331.gif)