 +
+  +
+  +
+  =
= 
 +
+  +
+  +
+  =
= 
This application proposes for you to visualize the following list of quadratic hypersurfaces in the space-time of dimension 4. In the equations, x,y,z are the coordinates of the space, and we use the variable t to designate the coordinate time. A same hypersurface is often presented several times, under different viewing angles (in particular with respect to t).
| equation | hypersurface |
|---|---|
| x*y*z-n=0 | corner hypersurface |
| z1.im*cos(a) + z2.im*sin(a) | Fermat hypersurface |
| [cosα cosγ,sinα cosγ,cosβ sinγ,sinβ sinγ] | flat tori |
A quadratic hypersurface is the set of points verifying an algebraic equation of degree 2.
Click the blue equation to load, manually change the t value by a slider.
| .gif | No. # | equation | description |
|---|---|---|---|
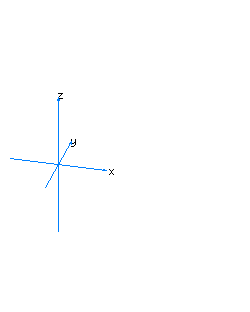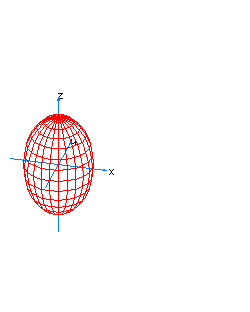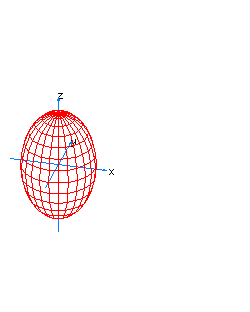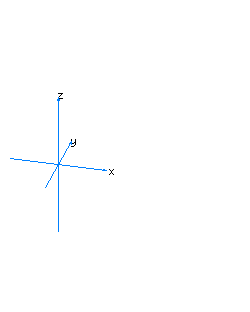 | 1 | x2+y2+z2+t2=1 | sphere S3 |
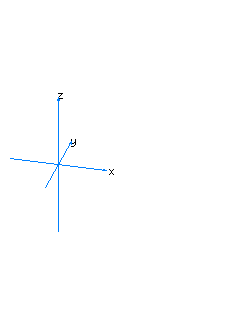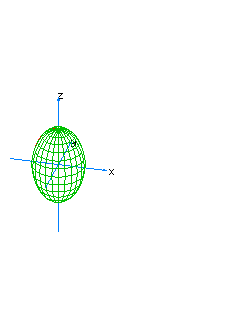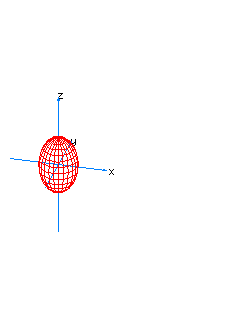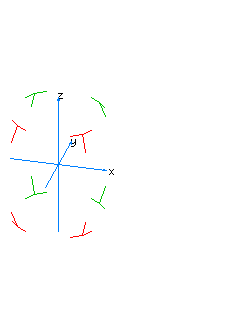 | 2 | x2+y2+z2-t2=0 | spherical cone with principal axis on the axis of t |
 | 3 | x2+y2-z2+t2=0 | spherical cone with principal axis on the axis of z |
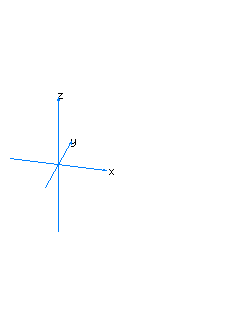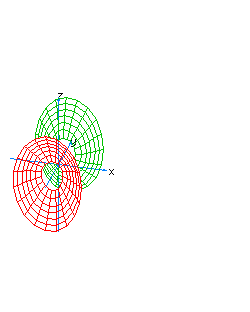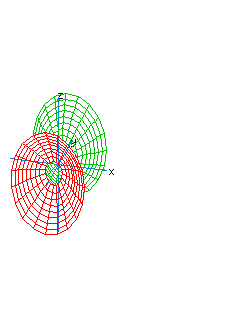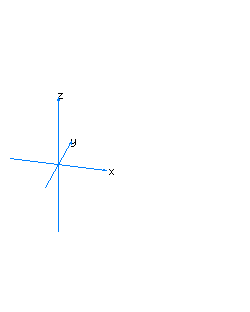 | 4 | x2-y2+z2+t2=0 | spherical cone with principal axis on the axis of y |
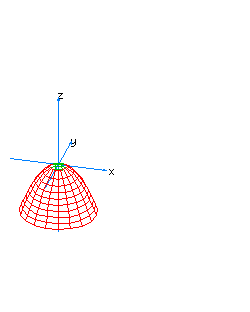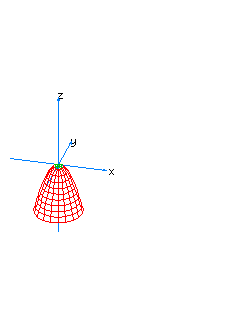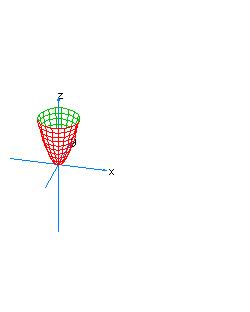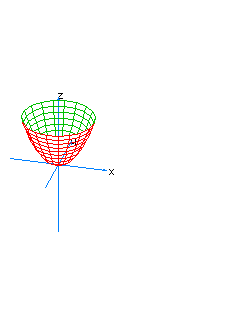 | 5 | x2+y2-z*t=0 | spherical cone whose principal axis is the line x=y=z+t=0 |
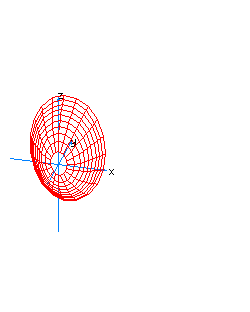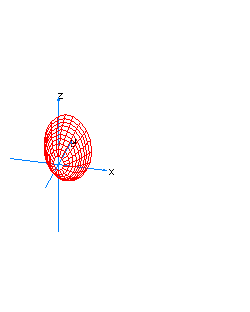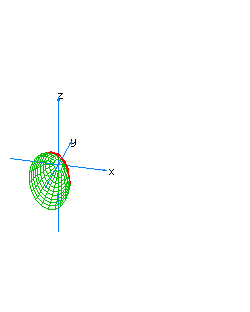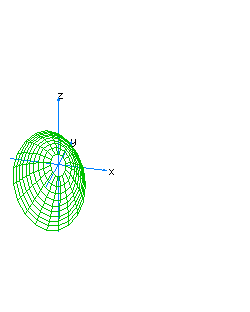 | 6 | x2+z2-y*t=0 | spherical cone whose principal axis is the line x=z=y+t=0 |
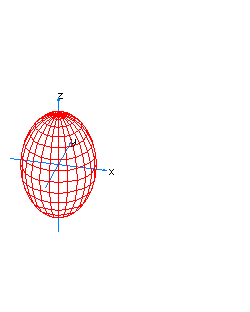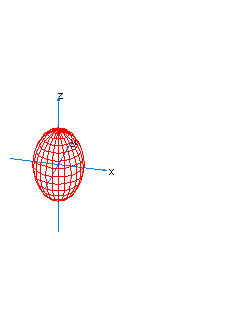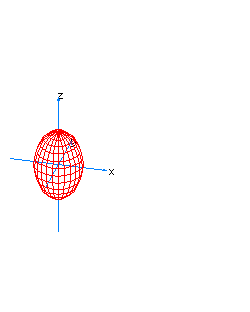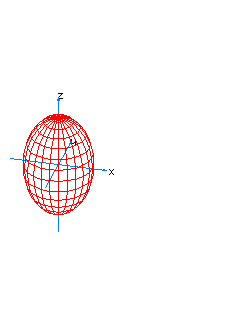 | 7 | x2+y2+z2-t2=1 | spherical hyperboloid whose principal axis is the axis of t |
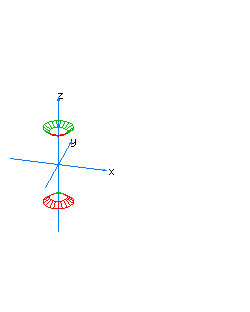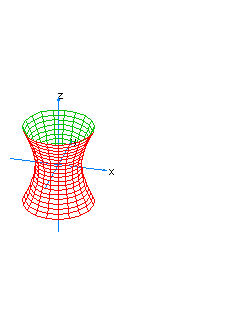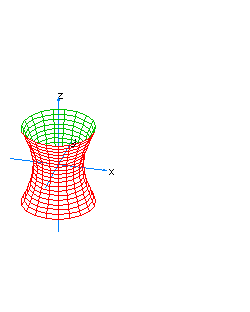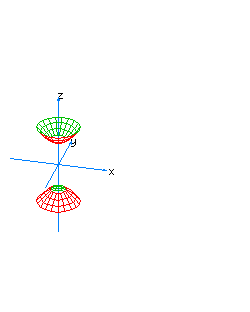 | 8 | x2+y2-z2+t2=1 | spherical hyperboloid whose principal axis is the axis of z |
 | 9 | x2-y2+z2+t2=1 | spherical hyperboloid whose principal axis is the axis of y |
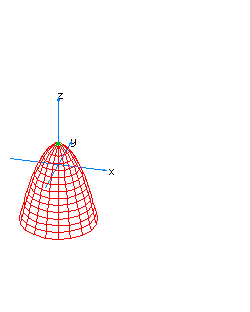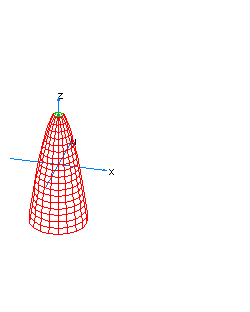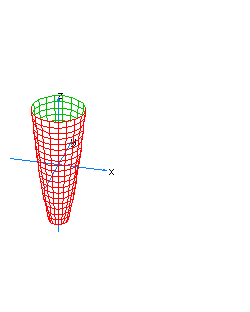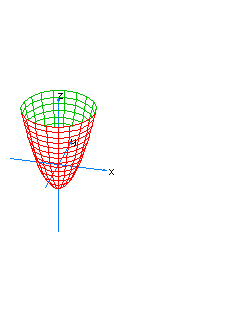 | 10 | x2+y2-z*t=1 | spherical hyperboloid whose principal axis is the line x=y=z+t=0 |
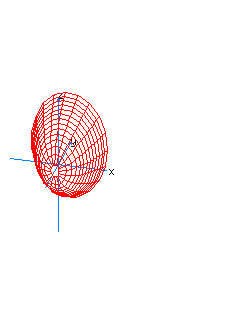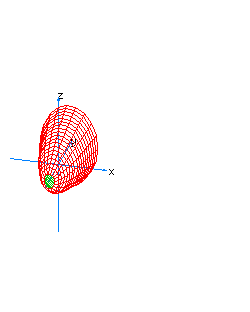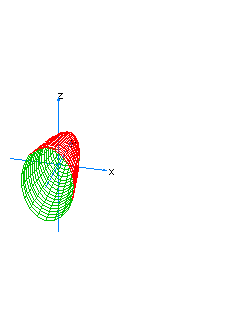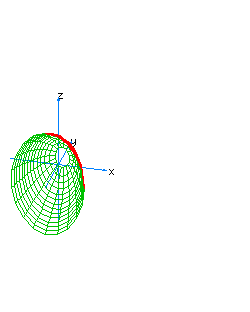 | 11 | x2+z2-y*t=1 | spherical hyperboloid whose principal axis is the line x=z=y+t=0 |
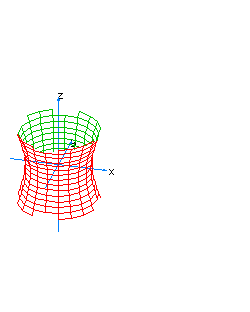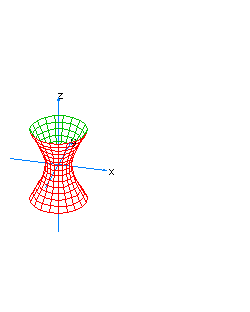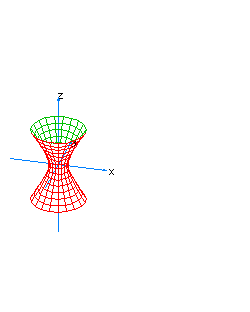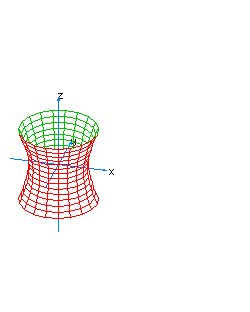 | 12 | x2+y2-z2-t2=0 | vertical hyperboloidal cone |
 | 13 | x2-y2+z2-t2=0 | horizontal hyperboloidal cone |
 | 14 | x2-y2-z*t=0 | hyperboloidal cone |
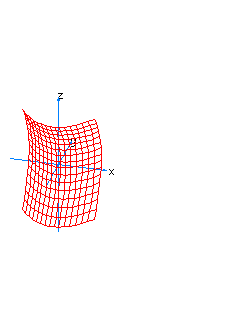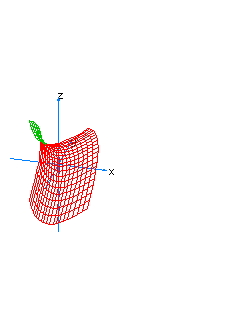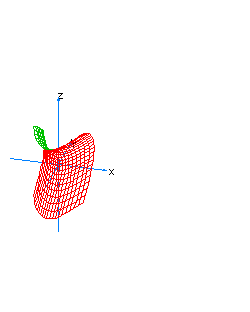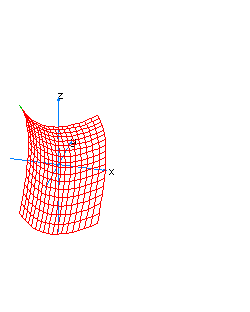 | 15 | x2-z2-y*t=0 | hyperboloidal cone |
 | 16 | x2+y2-z2-t2=1 | hyperboloidal hyperboloid |
 | 17 | x2-y2+z2-t2=1 | hyperboloidal hyperboloid |
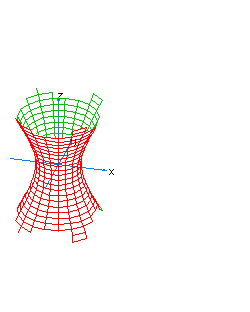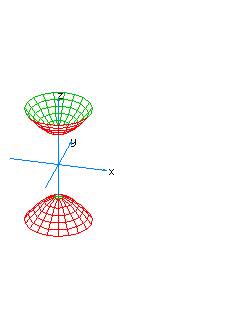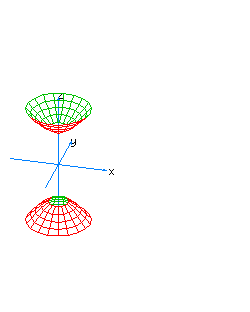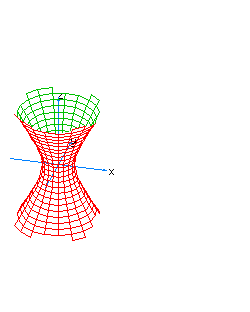 | 18 | x2+y2-z2-t2= -1 | hyperboloidal hyperboloid |
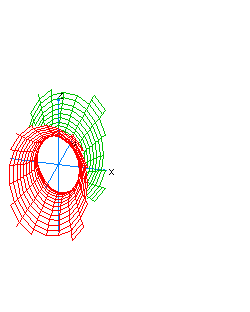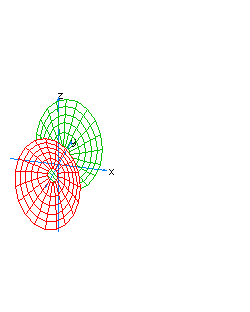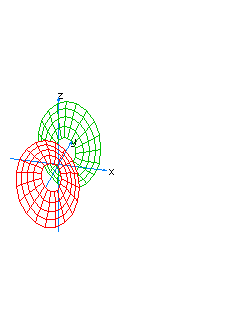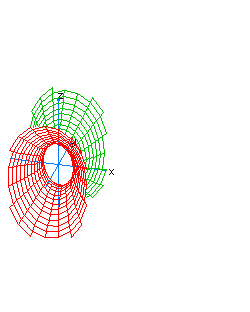 | 19 | x2-y2+z2-t2= -1 | hyperboloidal hyperboloid |
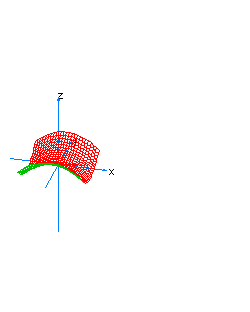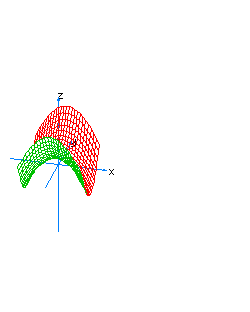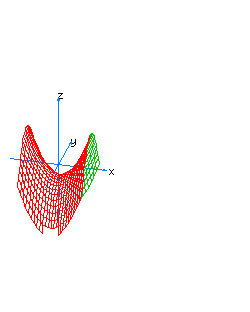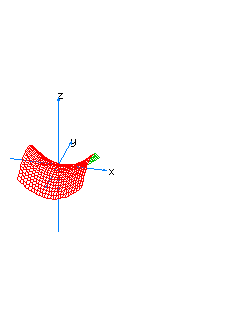 | 20 | x2-y2-z*t=1 | hyperboloidal hyperboloid |
 | 21 | x2-z2-y*t=1 | hyperboloidal hyperboloid |
 | 22 | x2+y2+z2-t=0 | spherical paraboloid oriented towards the axis of t |
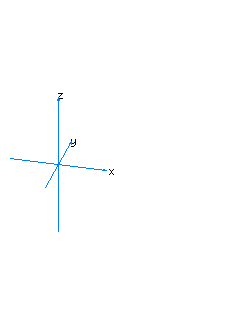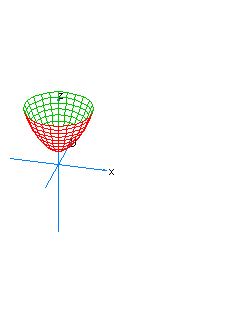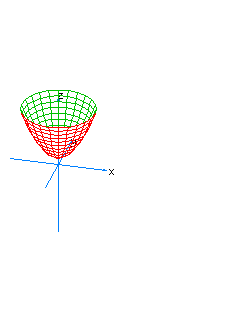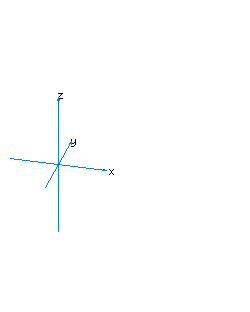 | 23 | x2+y2-z+t2=0 | spherical paraboloid oriented towards the axis of z |
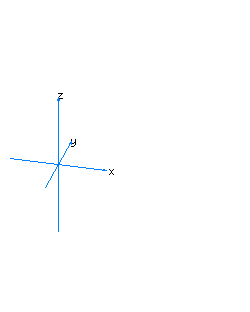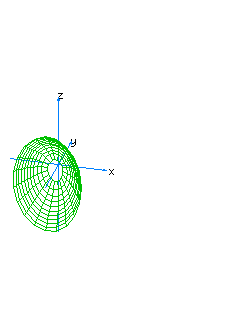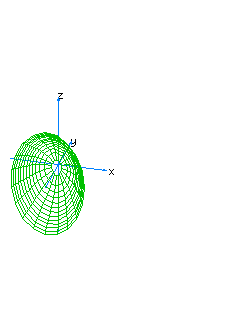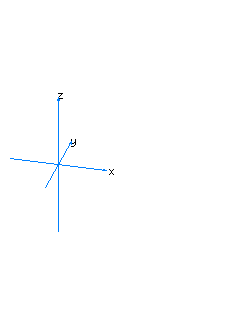 | 24 | x2-y+z2+t2=0 | spherical paraboloid oriented towards the axis of y |
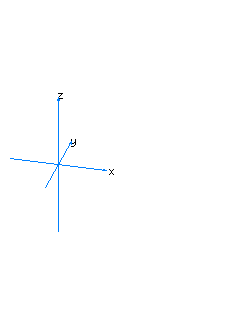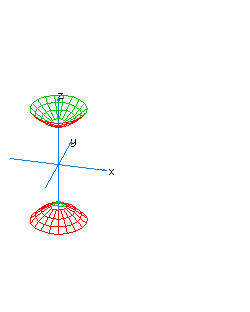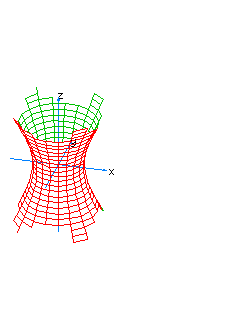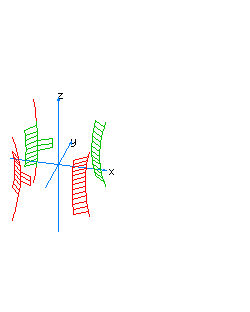 | 25 | x2+y2-z2-t=0 | hyperboloidal paraboloid oriented towards the axis of t, vertical |
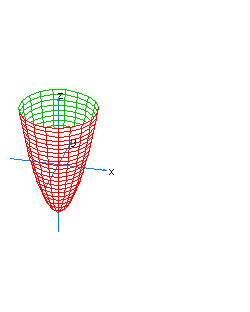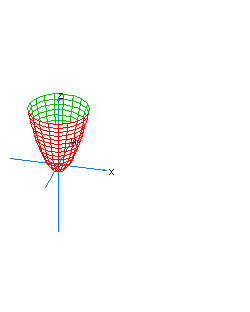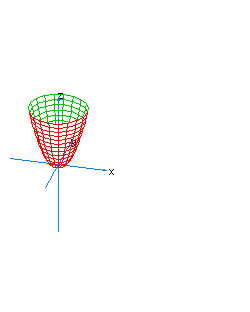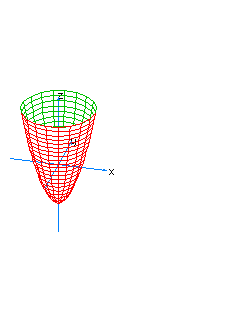
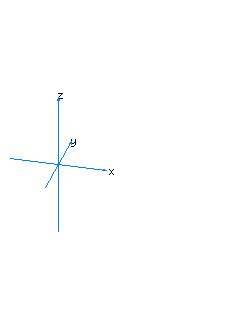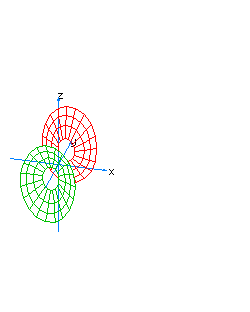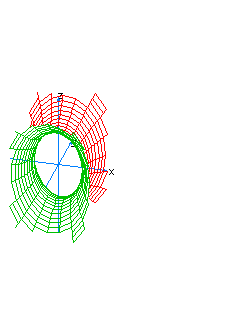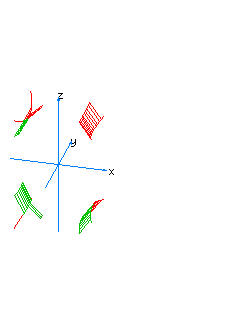 | 26 | x2-y2+z2-t=0 | hyperboloidal paraboloid oriented towards the axis of t, horizontal |
 | 27 | x2+y2-z-t2=0 | hyperboloidal paraboloid oriented towards the axis of z |
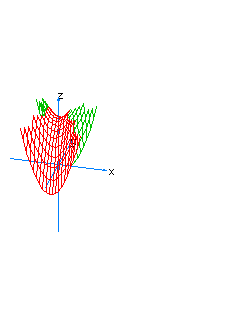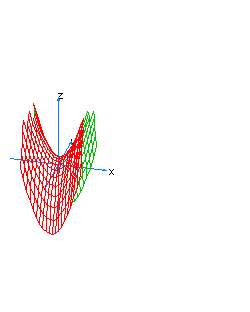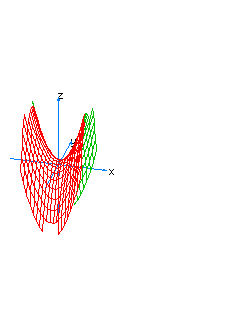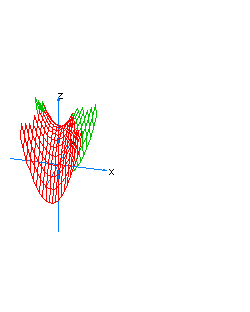 | 28 | x2-y2-z+t2=0 | hyperboloidal paraboloid oriented towards the axis of z |
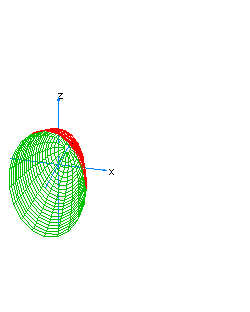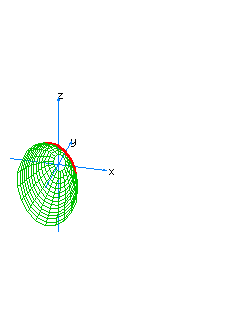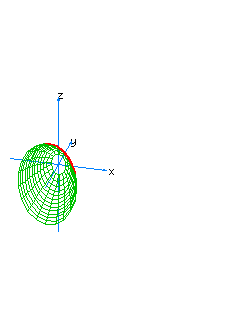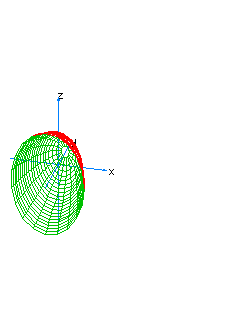 | 29 | x2-y+z2-t2=0 | hyperboloidal paraboloid oriented towards the axis of y |
 | 30 | x2-y-z2+t2=0 | hyperboloidal paraboloid oriented towards the axis of y |
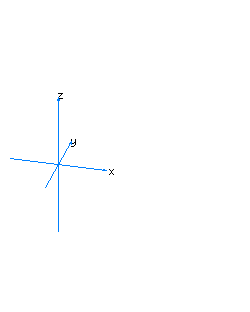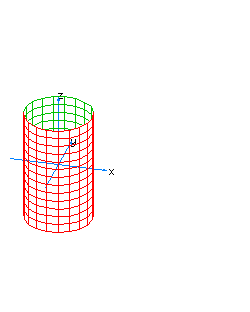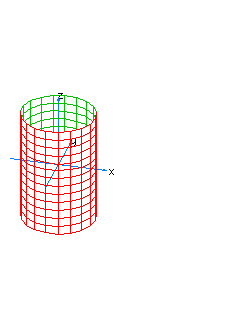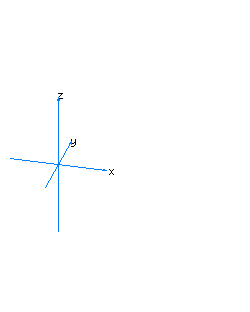 | 31 | x2+y2+t2=1 | vertical spherical cylinder |
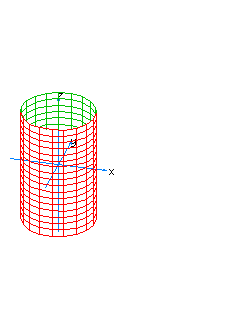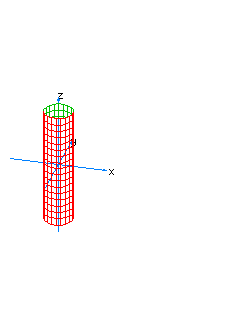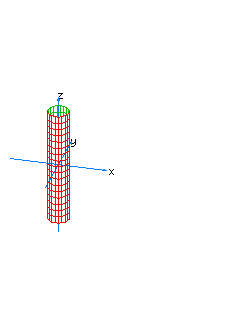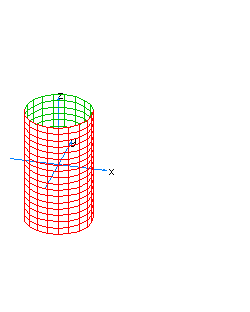
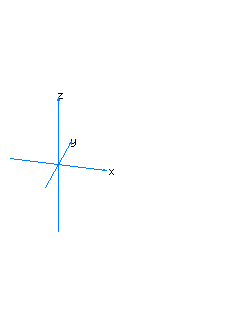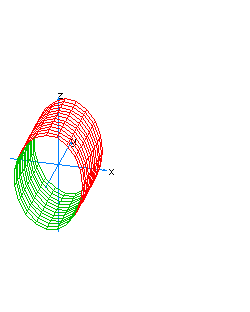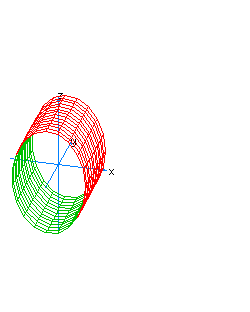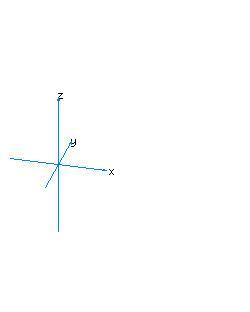 | 32 | x2+z2+t2=1 | horizontal spherical cylinder |
 | 33 | x2+y2-t2=0 | conic cylinder with a singular line on the axis of z |
 | 34 | x2+z2-t2=0 | conic cylinder with a singular line on the axis of y |
 | 35 | x2+y2-t2=1 | hyperboloidal cylinder with one sheet, vertical |
 | 36 | x2+z2-t2=1 | hyperboloidal cylinder with one sheet, horizontal |
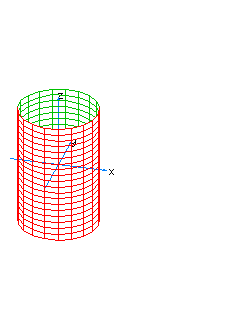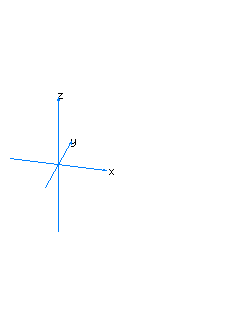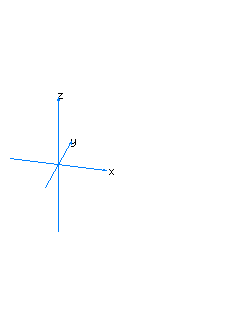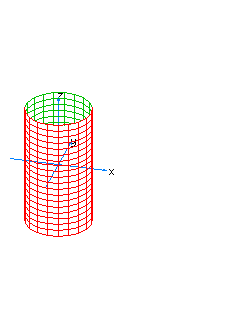 | 37 | x2+y2-t2=1 | hyperboloidal cylinder with two sheets, vertical |
 | 38 | x2+z2-t2=1 | hyperboloidal cylinder with two sheets, horizontal |
| ? | 39 | x*y*z-t=0 | corner hypersurface |