|
|
|
Given a Circle ![]() with Center
with Center ![]() and Radius
and Radius ![]() , then two points
, then two points ![]() and
and ![]() are inverse with
respect to
are inverse with
respect to ![]() if
if
![]() . If
. If ![]() describes a curve
describes a curve ![]() , then
, then ![]() describes a curve
describes a curve ![]() called the inverse
of
called the inverse
of ![]() with respect to the circle
with respect to the circle ![]() (with Inversion Center
(with Inversion Center ![]() ). If the Polar
equation of
). If the Polar
equation of ![]() is
is ![]() , then the inverse curve has polar equation
, then the inverse curve has polar equation
![$\displaystyle x_0+{k^2(f-x_0])\over(f-x_0)^2+(g-y_0)^2}$](i_962.gif) |
|||
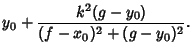 |
See also Inversion, Inversion Center, Inversion Circle
References
Lee, X. ``Inversion.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Inversion_dir/inversion.html.
Lee, X. ``Inversion Gallery.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/InversionGallery_dir/inversionGallery.html
Yates, R. C. ``Inversion.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 127-134, 1952.
|
|
|
© 1996-9 Eric W. Weisstein